「一次独立・一次従属とは?」では,ベクトル空間を考えるうえでとても重要な概念である,一次独立と一次従属について勉強します.
後に学習していくとわかることですが,この一次独立と一次従属は集合の広がり度合いを調べることができるものです.
ベクトル空間の中でとても重要なテーマなのでしっかりと学んでいきましょう!
この記事では,一次独立とは何かという話にとどまり実際に一次独立性を計算することはありません.
実際の一次独立の計算が気になりましたら「同次連立一次方程式と一次独立性」や「rankと一次独立性」の記事を参照してください!
・一次独立と一次従属の定義を理解する.
・一次独立と一次従属の図形的意味を理解する.
一次独立と一次従属
一次独立と一次従属
ベクトル空間のn個のベクトル\( \mathbf{a_1,a_2, \cdots ,a_n} \)と
n個のスカラー\( c_1,c_2 \cdots c_n \in \mathbb{R} \)に対して
\( c_1\mathbf{a_1}+c_2\mathbf{a_2}+ \cdots +c_n\mathbf{a_n} = \mathbf{0} \)
が成り立つのが、
\( c_1 = c_2 = \cdots = c_n = 0 \)のみのとき,
\( {\mathbf{a_1,a_2, \cdots ,a_n}} \)は一次独立という.
また,一次独立ではない.すなわち,
\( c_1,c_2 \cdots c_n \)のうち少なくとも1つは0ではないものがあるとき
\( {\mathbf{a_1,a_2, \cdots ,a_n}} \)は一次従属という.
この定義から何が言えるのか図も使って考察していきましょう.
\( c_1\mathbf{a_1}+c_2\mathbf{a_2}+ \cdots +c_n\mathbf{a_n} = \mathbf{0} \cdots (\heartsuit) \)に対して,
一次従属だった場合「\( c_1,c_2 \cdots c_n \)のうち少なくとも1つは0ではないものがある」
といっていますので,
仮に\( c_n \neq 0 \)としてみます.
そうすると
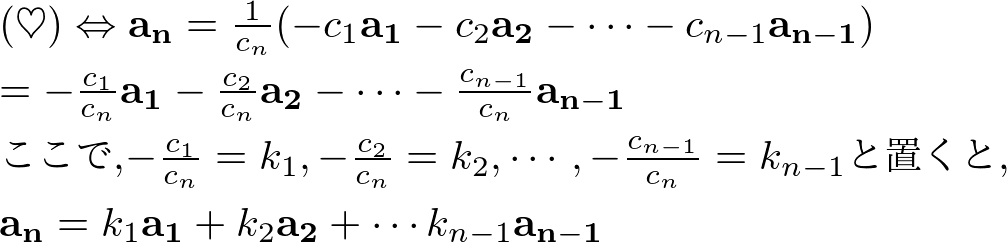
と書き換えられます.
すなわち,一次従属のときベクトル空間のn個のベクトルの内,
どれかのベクトル\( a_k(1\leq k \leq n) \)は
残りのn-1本のベクトルの一次結合で書くことができる.
と言い換えられます.
また,一次独立の時は\( c_1 = c_2 = \cdots = c_n = 0 \)となりますので,
0で割り算することはできませんから
一次独立のときベクトル空間のn個のベクトルのうち
どのベクトル\( a_k(1\leq k \leq n) \)も
残りのn-1本のベクトルの一次結合で書くことはできない.
と言い換えることが可能です.
ではさらにこのことから何がわかるのか,
実際にn=2の場合とn=3の場合を例に図を書いてかんがえていきます.
・n=2のとき
ベクトル空間\( \mathbb{R}^{2} \)に対して,
\( \mathbf{a},\mathbf{b}\in \mathbb{R}^{2} \)をとる.
\( c_1,c_2 \in \mathbb{R} \)を用いて一次結合\( c_1\mathbf{a} + c_2\mathbf{b} = \mathbf{0} \)とあらわしたときに
\( \mathbf{a},\mathbf{b} \)が一次従属であることは,以下のように書ける.
\( \mathbf{a},\mathbf{b} \)が一次従属
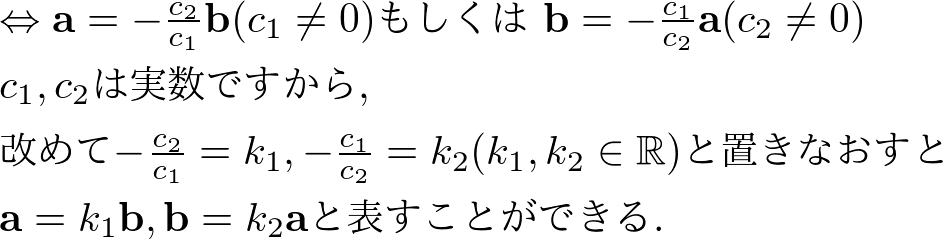
すなわちこれは\( \mathbf{a},\mathbf{b} \)が一次従属であれば,
\( \mathbf{a},\mathbf{b} \)が同一直線上にあることを表していますね.
では,一次独立な場合はどうなるでしょうか.
この場合は\( c_1 = 0,c_2 = 0 \)ですからどう頑張っても
\( \mathbf{a} = k \mathbf{b}(k \in \mathbb{R}) \)または\( \mathbf{b} = l \mathbf{a}(l \in \mathbb{R}) \)
という形は作れません.
つまりこれは,同一直線上にないことを表しています.
以上のことをまとめておきましょう.
n = 2のとき
\( \mathbf{a},\mathbf{b}\in \mathbb{R}^{2} \)が
一次従属\( \Leftrightarrow \) \( \mathbf{a},\mathbf{b} \)は同一直線上にある.
一次独立\( \Leftrightarrow \) \( \mathbf{a},\mathbf{b} \)は同一直線上にない.
・n=3のとき
ベクトル空間\( \mathbb{R}^{3} \)に対して,
\( \mathbf{a},\mathbf{b},\mathbf{c} \in \mathbb{R}^{3} \)をとる.
\( t_1,t_2,t_3 \in \mathbb{R} \)を用いて
一次結合\( t_1\mathbf{a} + t_2\mathbf{b} + t_3\mathbf{c}= \mathbf{0} \)とあらわしたときに
\( \mathbf{a},\mathbf{b},\mathbf{c} \)が一次従属であることは,以下のように書ける.
\( \mathbf{a},\mathbf{b},\mathbf{c} \)が一次従属

すなわちこのことは
\( \mathbf{a} \)が\( \mathbf{b},\mathbf{c} \)の一次結合でかけるといっていますので,
\( \mathbf{a},\mathbf{b},\mathbf{c} \)が同一平面上にあることを表していますね.
イメージは以下の図です
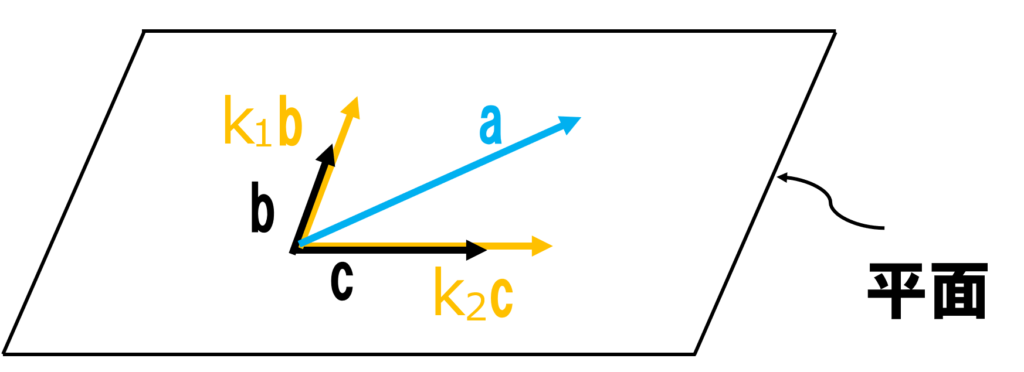
では,一次独立な場合はどうなるでしょうか.
n = 2の時と同様にこの場合は\( t_1 = 0,t_2 = 0,t_3 = 0 \)ですからどう頑張っても
\( \mathbf{a} = l_1 \mathbf{b} + l_2\mathbf{c}(l_1,l_2 \in \mathbb{R}) \)という形は作れません.
つまりこれは,
\( \mathbf{a},\mathbf{b},\mathbf{c} \)は同一平面上にないことを表しています.
イメージは以下の図です
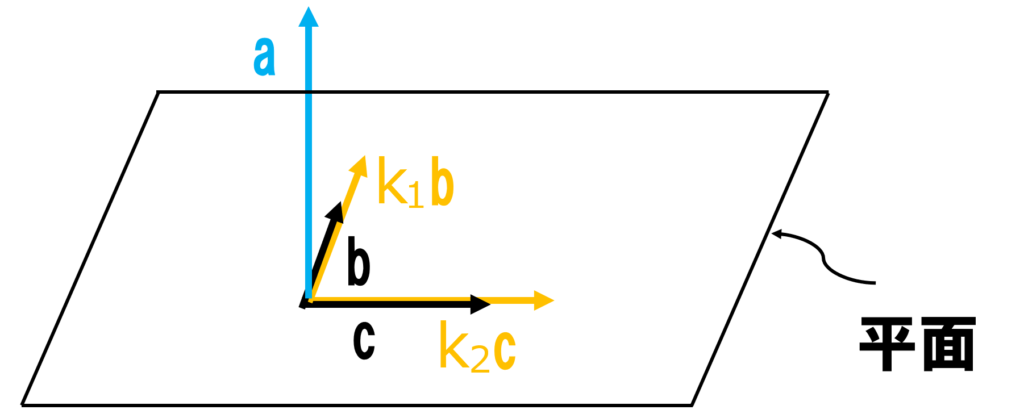
以上のことをまとめておきましょう.
・n = 3のとき
\( \mathbf{a},\mathbf{b},\mathbf{c}\in \mathbb{R}^{3} \)が
一次従属\( \Leftrightarrow \) \( \mathbf{a},\mathbf{b} \)は同一平面上にある.
一次独立\( \Leftrightarrow \) \( \mathbf{a},\mathbf{b} \)は同一平面上にない.
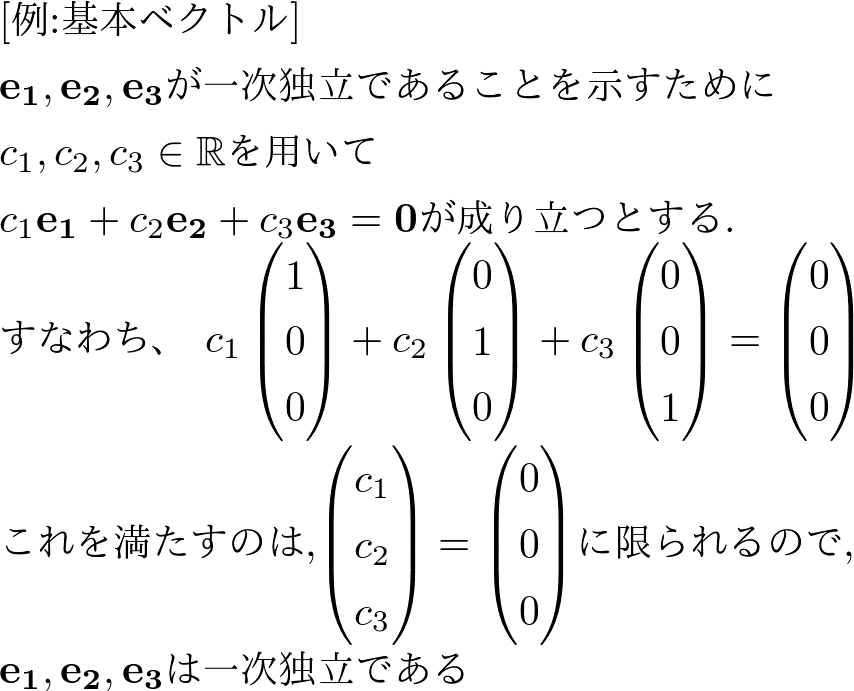
例:基本ベクトル
\( \mathbb{R}^3 \)の基本ベクトル\( \mathbf{e_1} = \begin{pmatrix} 1
\\0
\\0 \end{pmatrix},\mathbf{e_2} = \begin{pmatrix} 0
\\1
\\0 \end{pmatrix},\mathbf{e_3} = \begin{pmatrix} 0
\\0
\\1 \end{pmatrix} \)は一次独立である.
定義より一次独立であるならば
\( c_1\mathbf{e_1}+c_2\mathbf{e_2} +c_n\mathbf{e_n} = \mathbf{0} \)
をみたすような\(c_1,c_2,c_3\)は
\((c_1,c_2,c_3) = (0,0,0)\)に限られることを示せばよいです.
では,確認していくことにしましょう!
以上が「一次独立・一次従属とは?」という話です冒頭にも書きましたがぜひ「同次連立一次方程式と一次独立性」や「rankと一次独立性」の記事に進んで見てください具体的な一次独立性の判定について解説しています.
それではまとめに入ります!
「一次独立・一次従属とは?」まとめ
ベクトル空間のn個のベクトル\( \mathbf{a_1,a_2, \cdots ,a_n} \)と
n個のスカラー\( c_1,c_2 \cdots c_n \in \mathbb{R} \)に対して
\( c_1\mathbf{a_1}+c_2\mathbf{a_2}+ \cdots +c_n\mathbf{a_n} = \mathbf{0} \)
が成り立つのが、
\( c_1 = c_2 = \cdots = c_n = 0 \)のみのとき,
\( {\mathbf{a_1,a_2, \cdots ,a_n}} \)は一次独立という.
\( c_1,c_2 \cdots c_n \)のうち少なくとも1つは0ではないものがあるとき
\( {\mathbf{a_1,a_2, \cdots ,a_n}} \)は一次従属という.
入門線形代数記事一覧は「入門線形代数」

