「同次連立一次方程式と一次独立性」では,同次連立一次方程式の自明解と非自明解を使って一次独立か一次従属かどうかを判断する方法を学んでいこうと思います!!
今回やる方法はrankによる一次独立性の判断にもつながるとても大切な単元ですので,しっかりとマスターしていきましょう!
この記事は「同次連立一次方程式と自明解」がベースになっていますので,同次連立一次方程式自明解と非自明解ってなんだっけという方はこちらの記事を復習すると良いでしょう.
・同次連立一次方程式と一次独立性の関係をしっかりとおさえる.
・同次連立一次方程式を用いて一次独立性を判断できるようになる
同次連立方程式による一次独立性の判定
まずは同次連立一次方程式での判断を行う前に
一次独立と一次従属について簡単に復習しておきましょう.
一次独立と一次従属
ベクトル空間のn個のベクトル\( \mathbf{a_1,a_2, \cdots ,a_n} \)と
n個のスカラー\( c_1,c_2 \cdots c_n \in \mathbb{R} \)に対して
\( c_1\mathbf{a_1}+c_2\mathbf{a_2}+ \cdots +c_n\mathbf{a_n} = \mathbf{0} \)が成り立つのが、
\( c_1 = c_2 = \cdots = c_n = 0 \)のみのとき,
\( {\mathbf{a_1,a_2, \cdots ,a_n}} \)は一次独立という.
また,一次独立ではない.すなわち,
\( c_1,c_2 \cdots c_n \)のうち少なくとも1つは0ではないものがあるとき
\( {\mathbf{a_1,a_2, \cdots ,a_n}} \)は一次従属という.
一次独立と一次独立の定義についてもっと詳しく勉強したい方は
こちらの「一次独立・一次従属とは?」の記事を参考にするとよいでしょう
では,ここからは同次連立一次方程式と一次独立性の関係を見ていくことにします.
同次連立一次方程式と一次独立性
同次連立一次方程式
\( A \mathrm{x} = 0 ,A = (\mathbf{a_1,a_2, \cdots ,a_n}) \)に関して,
・解が自明解のみである.すなわち,\(\mathrm{x} = 0\)
のとき,\(\mathbf{a_1,a_2, \cdots ,a_n}\)は一次独立である.
・解が非自明解を持つ.すなわち\(\mathrm{x} \neq 0 \)
となる解を持つとき,\(\mathbf{a_1,a_2, \cdots ,a_n}\)は一次従属である.
一次独立性は自明解のみを持つのか非自明解を持つのかに依存して決まることを言っています.
なぜ,この条件になるのかは問を通して理解していくのが良いかと思いますので,
下の問を通して考察していきましょう.
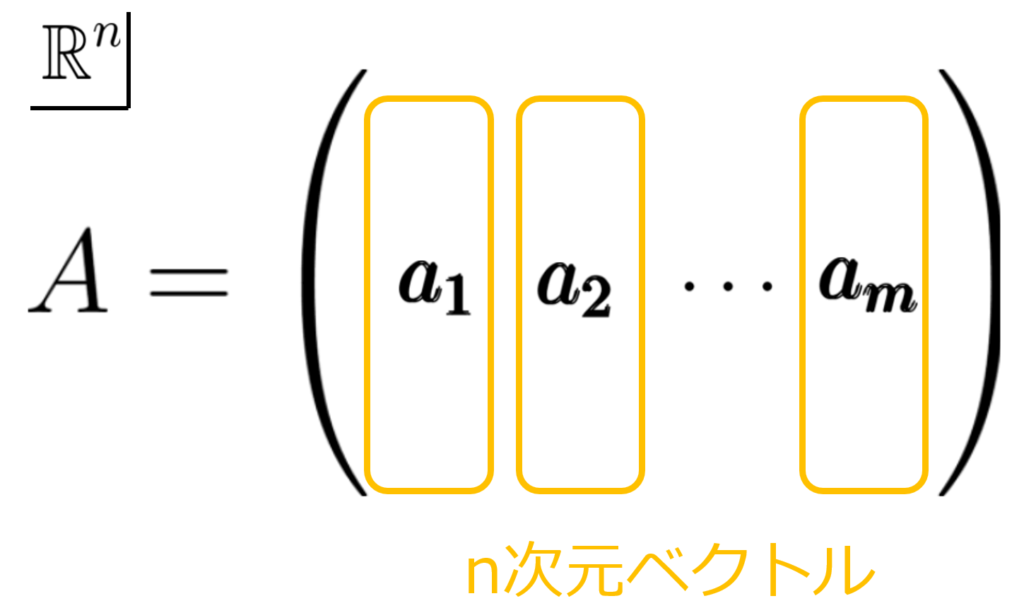
また,さりげなく書いてある\(A = (\mathbf{a_1,a_2, \cdots ,a_n}) \)
列ベクトル\(\mathbf{a_1,a_2, \cdots ,a_n}\)を並べたものが
行列Aであるということです.
図を用いると下のようになります
では,ここからは実際に問を解きつつ
一次独立性を確認していきましょう.
問:同次連立一次方程式と一次独立性
\( \mathbb{R}^3 \)のベクトル
\( \mathbf{a_1} = \begin{pmatrix} 1
\\1
\\0 \end{pmatrix},\mathbf{a_2} = \begin{pmatrix} 0
\\1
\\1 \end{pmatrix},\mathbf{a_3} = \begin{pmatrix} 1
\\1
\\1 \end{pmatrix},
\mathbf{a_4} = \begin{pmatrix} -1
\\0
\\1 \end{pmatrix} \)
に対して,
\(\mathbf{a_1,a_2,a_3}\)が一次独立,\(\mathbf{a_1,a_2,a_4}\)が一次従属
であることを示せ.


この問から,自明解を持つとき連立一次方程式の解は一次独立の条件を満たしていること
また非自明解を持てば解は任意定数を用いて表すことになるので,一次従属の条件を満たすこと
が確認できるのではないでしょうか
このように同次連立一次方程式と一次独立性は密接に絡んでいます.
このことを念頭に置いてrankによる一次独立性の判定もありますので,
そちらも併せて勉強するとより理解が深まるでしょう!
それではまとめに入ります!
「同次連立方程式と一次独立性」まとめ
同次連立一次方程式
\( A \mathrm{x} = 0 ,A = (\mathbf{a_1,a_2, \cdots ,a_n}) \)に関して,
・解が自明解のみである.すなわち,\(\mathrm{x} = 0\)
のとき,\(\mathbf{a_1,a_2, \cdots ,a_n}\)は一次独立である.
・解が非自明解を持つ.すなわち\(\mathrm{x} \neq 0 \)
となる解を持つとき,\(\mathbf{a_1,a_2, \cdots ,a_n}\)は一次従属である.
入門線形代数記事一覧は「入門線形代数」

