今回は, 階段行列という行列を紹介します.
階段行列はこの先行列のrankというものを計算したり, 他の概念を理解する上でとても大切な行列です. 階段行列をしっかり理解し, 判別もできるようになるように頑張りましょう!
この記事では「行列の主成分」がわからないとよく理解できないので, 行列の主成分を復習してから読むと良いでしょう.
・階段行列を理解し, 判別できるようになる.
階段行列
早速, 階段行列を定義していきます.
階段行列
行番号が増えていくにつれて主成分の前(左側)に連続して並ぶ0の数が増えていき, 主成分のない行より下の行はすべて成分が0であるような行列のことを階段行列という.
文章だけではイメージしにくいと思うので, 具体例で確認していくことにします.
例:階段行列
以下の3つの行列は全て階段行列である.
\( \left(\begin{array}{ccccccc} 0 & a_1 & * & * & * & *
\\ 0 & 0 & a_2 & * & * & *
\\ 0 & 0 & 0 & a_3 & * & *
\\ 0 & 0 & 0 & 0 & a_4 & *
\\ 0 & 0 & 0 & 0 & 0 & a_5\end{array} \right) \),
\( \left(\begin{array}{cccccc}0 & a_1 & * & * & * & *
\\0 & 0 & a_2 & * & * & *
\\0 & 0 & 0 & 0 & 0 & a_3
\\0 & 0 & 0 & 0 & 0 & 0
\\0 & 0 & 0 & 0 & 0 & 0\end{array} \right) \),
\( \left(\begin{array}{cccccc}0 & a_1 & * & * & * & *
\\0 & 0 & 0 & 0 & a_2 & *
\\0 & 0 & 0 & 0 & 0 & 0
\\0 & 0 & 0 & 0 & 0 & 0
\\0 & 0 & 0 & 0 & 0 & 0\end{array} \right) \)
ただし, \( a_1, a_2, a_3, a_4, a_5 \)は全て0でなく, \( * \)の部分は好き勝手決めていい数が入るとする.
この例について, 図を用いることで視覚的に階段行列になっているか確認しましょう.


この行列は, 一行下がるごとに1つずつ主成分の前に0が増えています.
一番典型的な階段行列の形であるといえるでしょう.
他にも例を見てみます.
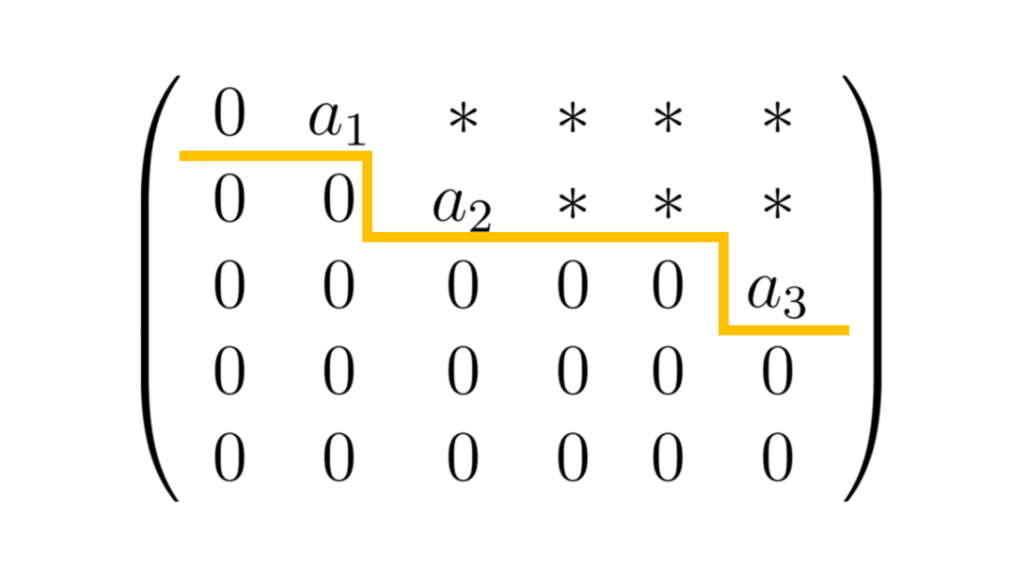
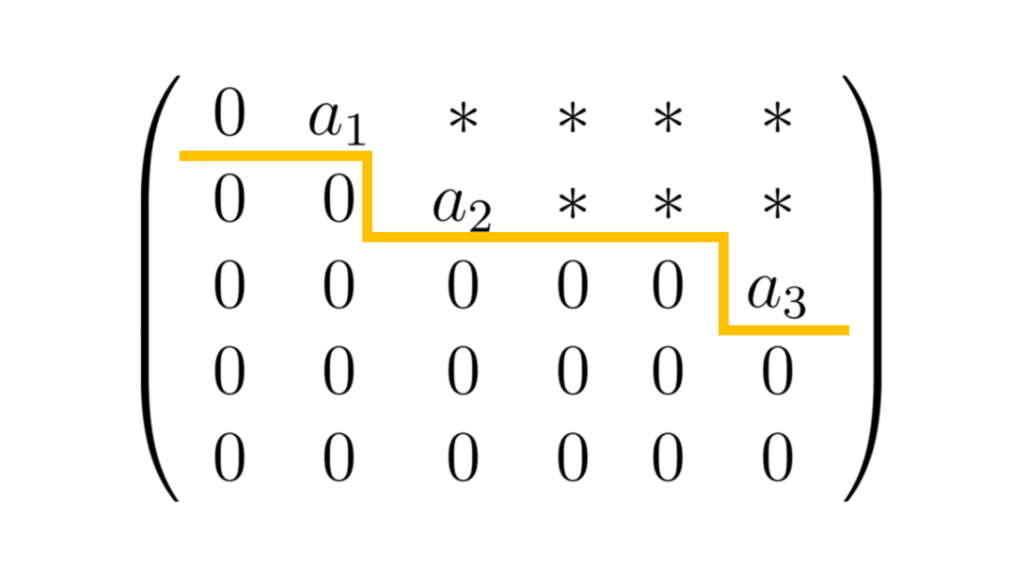
この行列は前の例のように, 等間隔で0が並んではいませんが, 行番号が増えるごとに0の数は増えています.
また, 主成分のない第4行目と5行目は0が並んでいるので, 階段行列になります.
最後の例について図は省略しますが, 上と同様に主成分の前の0の数がどんどん増えおり, 主成分のない3行目以降は0が並んでいるので, 問題なく階段行列です.
階段行列でない行列の例も見てみましょう.
例:階段行列でない行列
次の行列は階段行列ではない.
\( \left(\begin{array}{cccccc}0 & a_1 & * & * & * & *
\\0 & 0 & a_2 & * & * & *
\\0 & a_3 & * & * & * & *
\\0 & 0 & 0 & 0 & a_4 & *
\\0 & 0 & 0 & 0 & 0 & a_5\end{array} \right) \),
\( \left(\begin{array}{cccccc}0 & a_1 & * & * & * & *
\\0 & 0 & 0 & 0 & a_2 & *
\\0 & 0 & 0 & 0 & 0 & 0
\\0 & 0 & 0 & 0 & 0 & 0
\\0 & a_5 & * & * & * & * \end{array} \right) \)
ただし, \( a_1, a_2, a_3, a_4, a_5 \)は全て0でなく, \( * \)の部分は好き勝手決めていい数が入るとする.
こちらの例もひとつずつ, どこがダメなのか考えてみることにしましょう.
<例の確認>
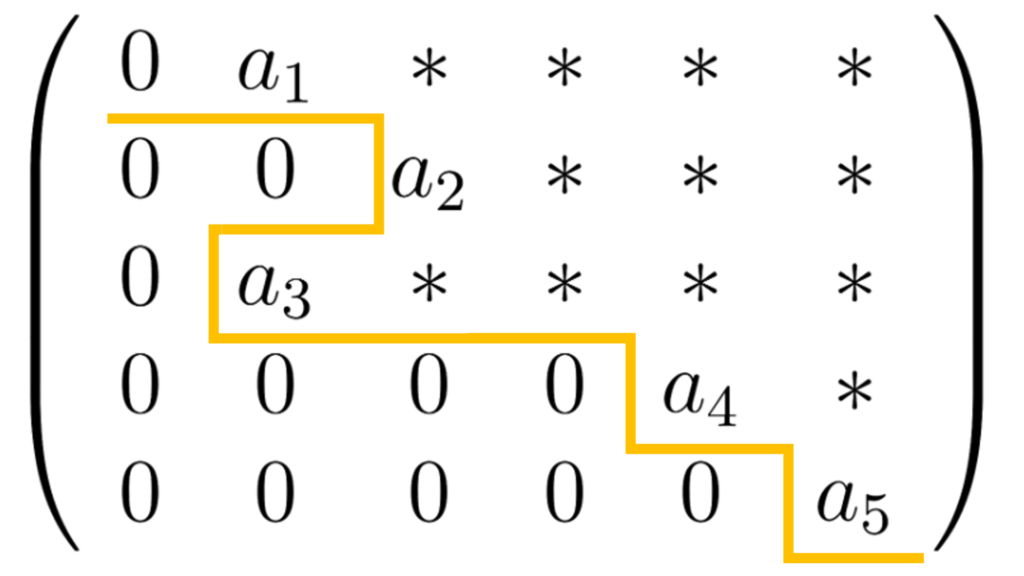
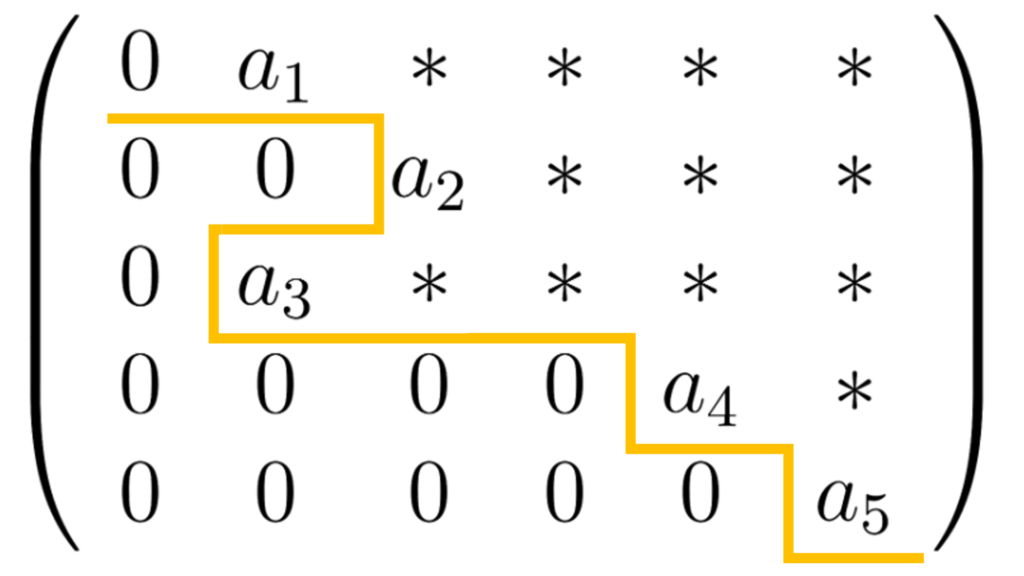
この行列では
第2行の主成分前には0が2つ
であるのに対して
第3行の主成分前には0が1つ
となってしまっているため,「階段行列の定義である行番号が増えていくにつれて, 主成分の前(左側)に連続して並ぶ0の数が増えていく」ということに反します.
よって, この行列は階段行列ではありません.
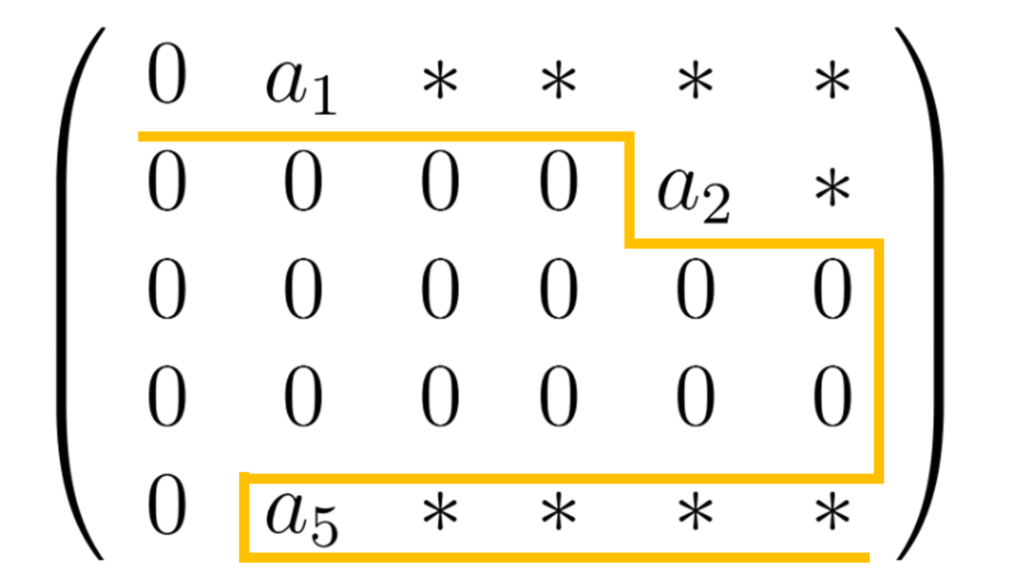

こちらの例も, いきなり第5行目で主成分前の0の数が1つに減ってしまっており, 「主成分のない行より下の行はすべて成分が0である」という階段行列の定義を満たさないので, 階段行列ではありません.
以上が階段行列についての解説です. この階段行列を用いて次回に解説する「階数(rank)」というものが定義されます.
それでは, 今回のまとめに入りましょう.
「階段行列」のまとめ
・階段行列とは, 行番号が増えていくにつれて主成分の前(左側)に連続して並ぶ0の数が増えていき, 主成分のない行より下の行はすべて成分が0であるような行列


