「rankと一次独立性」では,rankを用いて一次独立かどうかを判定していくということをやっていこうと思います.
この記事は「同次連立一次方程式と一次独立性」と非常に関連があるのでそちらの記事も参考にして学習を進めるとより理解が深まります
・rankと一次独立性の関係を理解する.
・rankを用いて一次独立かどうかを計算できるようになる.
rankによる一次独立性
早速一次独立とrankの関係をまとめていきましょう.
rankについて復習したい方は「行列の階数(rank)」を復習するとよいでしょう.
rankによる一次独立性
\( \mathbb{R}^n \)のm本のベクトル\( \mathbf{a_1},\mathbf{a_2},\cdots,\mathbf{a_m} \)を列ベクトルとする
n×m型行列\( A \)に対して,
\( \mathbf{a_1},\mathbf{a_2},\cdots,\mathbf{a_m} \)が一次独立\( \Leftrightarrow \mathrm{rank}A = m \)
とくに,m=nすなわち\( A \)がn×n型行列(n次正方行列)のとき
\( \mathbf{a_1},\mathbf{a_2},\cdots,\mathbf{a_n} \)が一次独立\( \Leftrightarrow \mathrm{rank} A = n \)
\( \mathbf{a_1},\mathbf{a_2},\cdots,\mathbf{a_n} \)が一次従属\( \Leftrightarrow \mathrm{rank} A < n \)
じつはこのことは,別記事「同次連立一次方程式と一次独立性」で勉強した
解の自明性と一次独立性についての議論をrankに焦点を当てて書いているだけです.
なので,このことの裏には同次連立一次方程式が潜んでいます.
では,実際に計算できるように例題と問を解いてみましょう.
例題:rankによる一次独立性
\( \mathbb{R}^4 \)において次のベクトルは一次独立か一次従属か判別せよ.
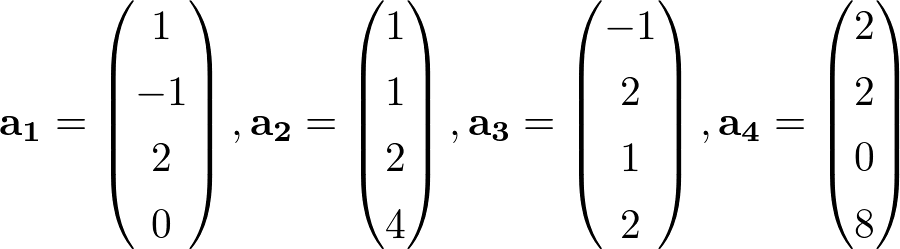
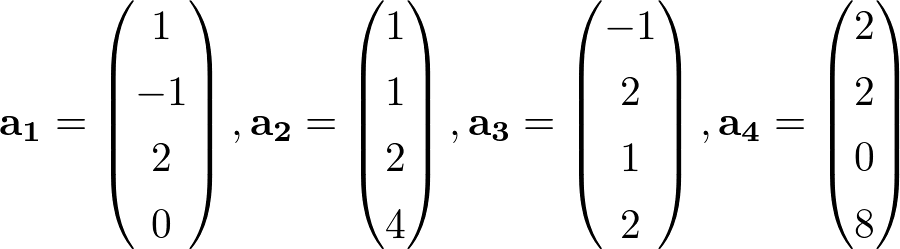


最終的に係数行列のrankとベクトルの本数を比べることを忘れないようにしてくださいね.
それでは,最後に問を解きましょう!
問:rankによる一次独立性
\( \mathbb{R}^4 \)において次のベクトルは一次独立か一次従属か判別せよ.
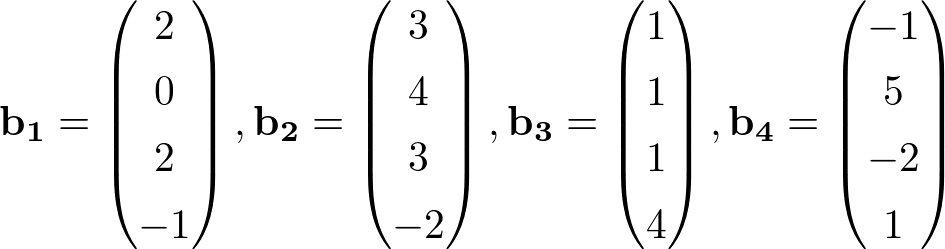
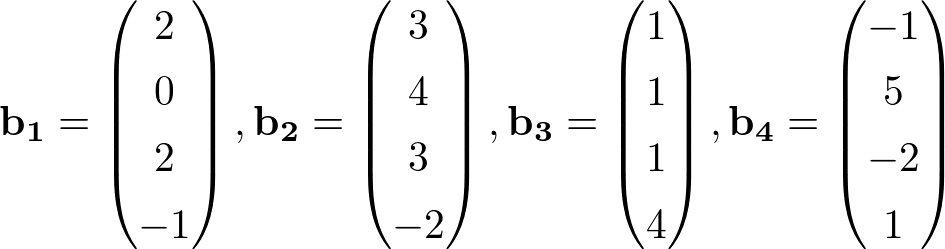


この例題と問を通して結局同次連立一次方程式と一緒じゃないかと思えた方は
しっかりと理解している方だと思います.
一次独立性の判別方法にはいろいろありますが,その時々で一番判定しやすいものを
用いることができるように各方法についてしっかりと理解指定おきましょう!
それではまとめに入ります!
「rankによる一次独立性」まとめ
\( \mathbb{R}^n \)のm本のベクトル\( \mathbf{a_1},\mathbf{a_2},\cdots,\mathbf{a_m} \)を列ベクトルとする
n×m型行列\( A \)に対して,
\( \mathbf{a_1},\mathbf{a_2},\cdots,\mathbf{a_m} \)が一次独立\( \Leftrightarrow \mathrm{rank}A = m \)
とくに,m=nすなわち\( A \)がn×n型行列(n次正方行列)のとき
\( \mathbf{a_1},\mathbf{a_2},\cdots,\mathbf{a_n} \)が一次独立\( \Leftrightarrow \mathrm{rank} A = n \)
\( \mathbf{a_1},\mathbf{a_2},\cdots,\mathbf{a_n} \)が一次従属\( \Leftrightarrow \mathrm{rank} A < n \)
入門線形代数記事一覧は「入門線形代数」


