「同次連立一次方程式と自明解」では,同次連立一次方程式の解を自明解と非自明解に分類して
性質を見ていくということをしていきます.
この自明解と非自明解は後に一次独立や一次従属の判定に使われる大切なものですので,是非ともしっかり学んでいきしょう!
・同次連立一次方程式とはなにか理解する
・同次連立一次方程式の解が自明解なのか非自明解なのか判断できるようになる
同次連立一次方程式
では最初に冒頭から出てきている同次連立一次方程式というものについて定義しましょう.
同次連立一次方程式
定数項がすべて0となる連立一次方程式のことを同次連立一次方程式という.
すなわち,\( A \mathrm{x} = 0 \)
連立一次方程式の定数項がすべて0ということは,連立一次方程式の形で書くと
以下のような連立一次方程式のことを言います.
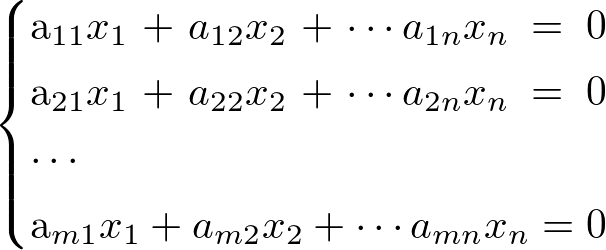
また,同次連立一次方程式は別の言い方で,”斉次連立一次方程式”とも言いますので,
覚えておきましょう.
では,次に連立一次方程式の解を見ていきましょう.
自明解と非自明解
同次連立一次方程式\( A \mathrm{x} = 0 \)に関して,
\( \mathrm{x} = 0 \)を自明解
\(\mathrm{x} \neq 0 \)を非自明解という.
そもそも連立一次方程式が解を持つ必要十分条件は,
連立一次方程式に対してAを係数行列\( (A | B) \)を拡大係数行列とするとき
\( \mathrm{rank}A = \mathrm{rank}(A \mid B) \) となることでした.(詳しくは「解の自由度と分類」で説明しています.)
同次連立一次方程式に関しては,
\( \mathrm{rank}A = \mathrm{rank}(A \mid 0) \)となりますので,
\( A \mathrm{x} = 0 \)は必ず解を持ちます.
特に\( \mathrm{x} = 0 \)は必ず解となり,この解のことを自明解と呼んでいます.
少し例を挙げてこの自明解と非自明解を具体的にイメージしてみましょう.
例:自明解と非自明解
同次連立一次方程式
\( \left\{\begin{array}{}x_{1} – 2x_{2} = 0
\\-2x_{1} + 4x_{2} = 0\end{array}\right. \)
は,\( \begin{pmatrix}x_{1}\\x_{2}\end{pmatrix} = \begin{pmatrix}0 \\0\end{pmatrix} \)を自明解として持ち,
一方,\( \begin{pmatrix}x_{1}\\x_{2}\end{pmatrix} = \begin{pmatrix}2\\1\end{pmatrix} \)を非自明解として持つ.

補足ですが,
この例では非自明解として,\( \begin{pmatrix}x_{1}\\x_{2}\end{pmatrix} = \begin{pmatrix}2\\1\end{pmatrix} \)をあげましたが,
非自明解はほかにも存在します.
もしよければご自身で探してみて下さい.
さて,定義の部分でもお話した通り,同次連立一次方程式は自明解を必ず解として持ちますので,
非自明解が持つか持たないかが大切です.
例を通して,自明解と非自明解がなんであるかはわかっていただけたかと思いますが,
実際に自明解を持つのか,非自明解を持つのか判断する方法
についてはまだ言及していません.
そこで,自明解を持つのか,非自明解を持つのかを判断する方法を定理として2つご紹介します.
定理:解の自明性とrank
まずは,rankをつかって自明性を確認する方法です.
未知数がn個の同次連立一次方程式\( A \mathrm{x} = 0 \)に対して
・\( A \mathrm{x} = 0 \)が自明解を持つ \( \Leftrightarrow \mathrm{rank}A = n\)
・\( A \mathrm{x} = 0 \)が非自明解を持つ \( \Leftrightarrow \mathrm{rank}A < n\)
この定理の証明は別の記事で示すことにします.
今回はこの定理を使って実際に判別する例を挙げておきます.


実際に掃き出し法を用いれば,(1)は自明解しか持たず,
(2)は任意定数を用いないと解が表せないので,非自明解を持つことがわかるかと思います.
定理:解の自明性と行列式
次に行列式を用いて解の自明性をかくにんする方法です.
未知数がn個の同次連立一次方程式\( A \mathrm{x} = 0 \)に対して
・\( A \mathrm{x} = 0 \)が自明解を持つ \( \Leftrightarrow \mathrm{det}A \neq 0\)
・\( A \mathrm{x} = 0 \)が非自明解を持つ \( \Leftrightarrow \mathrm{det}A = 0\)
この定理の証明も別の記事で示すことにします.
今回はこの定理を使って上と同じ問題を判別するしてみましょう.


以上が「同次連立一次方程式」の話です!!
正直子の話だけでは,うま味はあまりありませんが,一次従属や一次独立を判断するときなどに
威力を発揮しますので,しっかり押さえておきましょう!
それではまとめに入ります!
「同次連立一次方程式」まとめ
・同次連立一次方程式とは,定数項がすべて0となる連立一次方程式のこと
・\( A \mathrm{x} = 0 \)に関して,
\( \mathrm{x} = 0 \)を自明解,\(\mathrm{x} \neq 0 \)を非自明解という.
・同次連立一次方程式が自明解を持つ条件は
\(\mathrm{rank}A = n\)または,\( \mathrm{det}A \neq 0\)
・非自明解を持つ条件は
\(\mathrm{rank}A < n\)または\(\mathrm{det}A = 0\)
入
次回の記事「同次連立一次方程式と一次独立性」
入門線形代数記事一覧は「入門線形代数」



