「直交行列と直交変換」では,直交行列という様々な場面で登場する行列を紹介し,その直交行列を使った線形変換である直交変換を紹介していきます!
・直交行列とはなにか理解すること
・直交変換とは何か理解すること
直交行列
直交行列
実数を成分として持つn次正方行列\(A\)が
\({}^t\!A A = A {}^t\!A = E\)
を満たすとき,\(A\)を直交行列という.
たまにこの条件を正則行列と間違えている人を見かけますので注意しましょう.
直交行列は転置をとります.
正則行列については「逆行列の求め方(余因子行列)」で解説しています.
では,実際に直交行列を見ていくことにしましょう.
例:直交行列
以下の行列\(A,B\)は直交行列である.
\(A = \left(\begin{array}{ccc}0 & 1 & 0
\\1 & 0 & 0
\\0 & 0 & 1\end{array}\right)\)
\(B = \left(\begin{array}{cc}\cos\theta & -\sin\theta
\\\sin\theta & \cos\theta\end{array}\right)\)
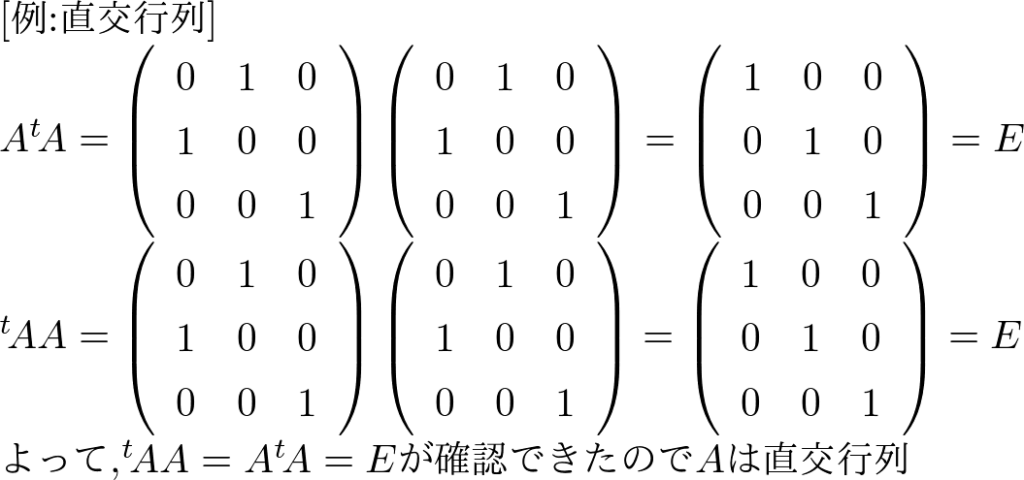
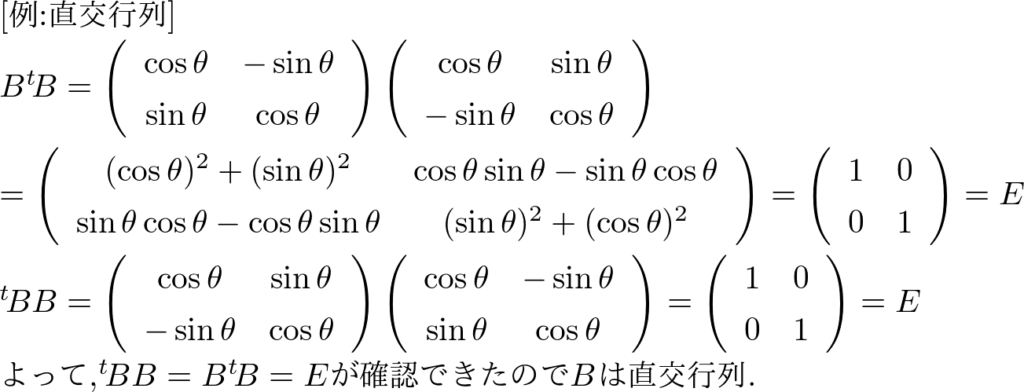
直交行列は線形代数の学習を進めていくと色々なところで条件として出てきます.意外と忘れがちなので,しっかり覚えておくとよいでしょう.
余談ですが,この行列\( B \)は回転行列といわれる行列で,この行列を用いるとベクトルを回転させることができます.よく微分幾何学等で見ます.
では,ここで直交行列に関する性質をいくつか挙げておきます
定理:直交行列の性質
実数を成分に持つn次正方行列\(A = (\mathbf{a_1} \cdots \mathbf{a_n})\)
\(A\)に対応する\(\mathbb{R^n}\)の線形変換\(f\)に対して,
以下の事は同値である.
(1)\(A\)は直交行列である.
(2)\(\left\{\mathbf{a_1} \cdots \mathbf{a_n} \right\}\)が行列\(A\)の列ベクトルであるとき,\(\left\{\mathbf{a_1} \cdots \mathbf{a_n} \right\}\)は\(\mathbb{R}^n\)の正規直交基底.
この定理を用いれば先ほどの「例:直交行列」で出てきた二つの行列の列ベクトルは正規直交基底ということができます.
直交行列はこのように正規直交基底と判断する際にも使われます
正規直交基底は「正規直交基底とグラムシュミットの直交化法」で解説しています.
直交変換
直交変換
実内積空間\(V\)の線形変換\(f:\mathbf{V}\rightarrow \mathbf{V}\)に対して,
\(\mathbf{V}\)の元\(\mathbf{a},\mathbf{b}\)が
\((f(\mathbf{a}),f(\mathbf{b})) = (\mathbf{a},\mathbf{b})\)
を満たすとき,\(f\)を直交変換という.
直交変換は直交変換の内積を求めても,ベクトルの内積を求めても結果が同じになるという少し不思議な奴です.
では,例を用いて直交変換を確認していきましょう.
例:直交変換
\(\mathbb{R}^3\)の線形変換
\(f(\begin{pmatrix} x_1
\\x_2
\\x_3 \end{pmatrix} ) = \begin{pmatrix}x_2
\\x_3
\\-x_1 \end{pmatrix} \)
は直交変換であることを確かめよ.

一度線形変換に対応する行列を用いて\(f(\mathbf{a}),f(\mathbf{b})\)を計算しましたが、パット計算してしまっても構いません.
さて実は、先ほど紹介した直交変換の定義「直交変換の内積を求めても,ベクトルの内積を求めても結果が同じになる」を用いると以下の定理が言えます.
定理:直交変換と直交行列
\(\mathbb{R}^n\)の線形変換\(f\)と,\(f\)に対応する行列を\(A\)とすると,
\(A\)が直交行列\(\Leftrightarrow\) \(f\)が直交変換
実は「例:直交変換」と「例:直交変換」は線形変換に対応する行列が直交行列になっています.
なぜだろうと思われた方は証明を行ってみるとより高い視点から見ることができるようになるのでお勧めです.
それでは、まとめに入ります!
「直交行列と直交変換」まとめ
・直交行列とは,\({}^t\!A A = A {}^t\!A = E\)
を満たす正方行列\( A \)
・直交変換とは,直交変換の内積を求めても,ベクトルの内積を求めても結果が同じになる線形変換
入門線形代数記事一覧は「入門線形代数」

