「逆行列の求め方(余因子行列)」では,逆行列という簡単に言うならば逆数の行列バージョンを
余因子行列という行列を用いて計算していくことになります.
この方法以外にも簡約化を用いた計算方法がありますが,それについては別の記事でまとめます
・逆行列とは何か理解すること
・余因子行列を用いて逆行列を計算できるようになること
この記事は一部(逆行列の定義の部分)が「逆行列の求め方(簡約化を用いた求め方)」
と重複しています.
逆行列
例えば実数の世界で2の逆数は?
と聞かれたら\( \frac{1}{2} \)と答えるかと思います.
言い換えると、\( 2 \times \frac{1}{2} = 1 \)が成り立ちます.
これを行列バージョンにしたのが逆行列です.
正則行列と逆行列
正方行列Aに対して
\( AX = XA = E \)を満たすXが存在するとき
Aは正則行列であるといい,
XをAの逆行列であるといい,\( A^{-1} \)とかく.
単位行列\( E \)は行列の世界でいうところの1に相当するものでしたので
定義の行列Xは行列Aの逆数のように捉えることができます.
ちなみに,\( A^{-1} \)は「Aインヴァース」と読みます.
また,ここでは深く触れませんが,正則行列に関しては学習を進めていくうえでいろいろなものの条件となったりする重要な行列ですのでしっかり押さえておきましょう.
逆行列の求め方(余因子行列を用いた求め方)
逆行列を定義していきますが,その前に余因子行列というものを定義します.
この余因子行列について間違えて覚えている人が非常に多いので
しっかりと定義をおぼえておきましょう.
余因子行列
n次正方行列Aに対して,
各成分の余因子を成分として持つ行列を転置させた行列
\( {}^t\!\widetilde{A}\)のことを行列Aの余因子行列という.
この定義だけではわかりにくいかと思いますので詳しく説明していきます.
行列の余因子に関してはこちらの記事を参照してください.
まず、各成分の余因子を成分として持つ行列とは
行列Aの各成分の余因子を\( A_{ij} \)として表したときに以下のような行列です.
\( \left(\begin{array}{cccc}A_{11} & A_{12} & \cdots & A_{1n} \\A_{21} & A_{22} & \cdots & A_{2n} \\& \cdots \cdots \\A_{n1} & A_{n2} & \cdots & A_{nn}\end{array}\right) = \widetilde{A} \)
ではこの行列の転置行列をとってみましょう.
\( \left(\begin{array}{cccc}A_{11} & A_{21} & \cdots & A_{n1} \\A_{12} & A_{22} & \cdots & A_{n2} \\& \cdots \cdots \\A_{1n} & A_{2n} & \cdots & A_{nn}\end{array}\right) = ^t\! \widetilde{A} \)
この\( ^t\! \widetilde{A} \)こそAの余因子行列です.
転置の操作を忘れてそのまま成分を書いてしまう人をよく見ますので注意してください.
必ず転置させて成分としてくださいね.
それではここからは実際に求め方に入っていきましょう
定理:逆行列の求め方(余因子行列を用いた求め方)
n次正方行列Aに対して
Aが正則行列の時Aの逆行列\( A^{-1} \)は
\( A^{-1} = \frac{1}{|A|}\widetilde{A} = \frac{1}{|A|}\left(\begin{array}{cccc}A_{11} & A_{21} & \cdots & A_{n1}
\\A_{12} & A_{22} & \cdots & A_{n2}
\\& \cdots \cdots
\\A_{1n} & A_{2n} & \cdots & A_{nn}\end{array}\right) \)である.
ここで,Aが正則行列であるということの必要十分条件は
Aが正則行列 \( \Leftrightarrow \) \( \mathrm{det}A \neq 0 \)
定理からもわかるように逆行列とは,
\(\frac{1}{|A|}\)を余因子行列に掛け算したものです.
ここで大切なのは正則行列であるということです.この条件がそもそも満たされていないと
逆行列は求めることができませんので注意してください.
それでは,実際に計算してみることにしましょう!
例題:逆行列の求め方(余因子行列を用いた求め方)
次の行列の逆行列を余因子行列を用いて求めなさい.
\( (1)A = \left(\begin{array}{cc}2 & 3
\\1 & 2\end{array}\right) \)
\( (2)B = \left(\begin{array}{crl}1 & 2 & 1
\\2 & 3 & 1
\\1 & 2 & 2\end{array}\right) \)
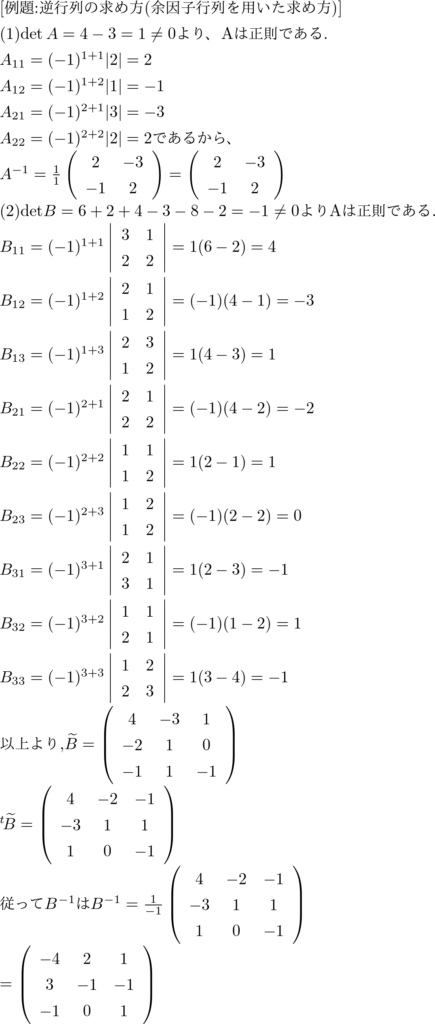
では,この例題を参考にして実際に問を解いてみることにしましょう!
問:逆行列の求め方(余因子行列を用いた求め方)
次の行列の逆行列を余因子行列を用いて求めなさい.
\( A = \left(\begin{array}{ccc}1 & 4 & 2
\\-1 & 1 & 3
\\-1 & -2 & 2\end{array} \right) \)
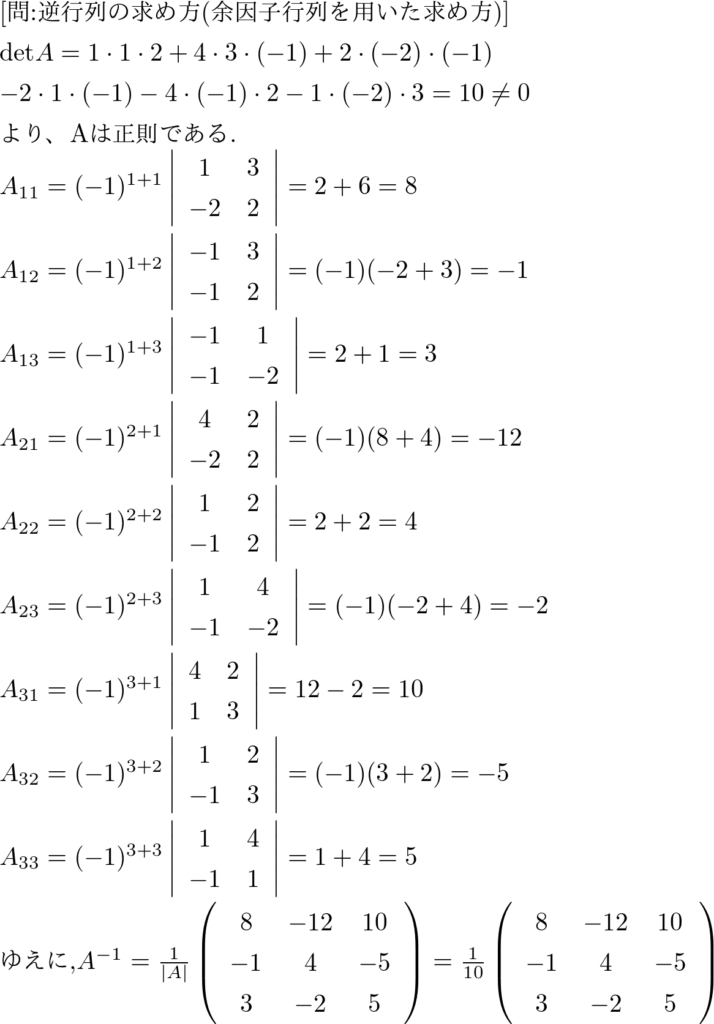
ここまでが、余因子を使った逆行列の求め方です.
意外と計算が多くて疲れますね笑
次の時期である逆行列の求め方(簡約化を用いた求め方)では少し違うアプローチになりますので,
ぜひこちらも一緒に勉強してみてください!
それではまとめに入ります!
「逆行列の求め方(余因子行列)」まとめ
・逆行列とは\( AX = XA = E \)を満たすXのことでそのXを\( A ^{-1} \)とかく.
・余因子行列とは,各成分の余因子を成分として持つ行列を転置させた行列
\( {}^t\!\widetilde{A}\)のこと
・Aが正則行列の時Aの逆行列\( A^{-1} \)は
\( A^{-1} = \frac{1}{|A|}\widetilde{A} = \frac{1}{|A|}\left(\begin{array}{cccc}A_{11} & A_{21} & \cdots & A_{n1}
\\A_{12} & A_{22} & \cdots & A_{n2}
\\& \cdots \cdots
\\A_{1n} & A_{2n} & \cdots & A_{nn}\end{array}\right) \)
入門線形代数記事一覧は「入門線形代数」

