「像(Image)と核(Kernel)」では,試験にも頻出の像と核について定義とその像と核を求めることをやっていこうと思います.
苦手としている方が多い分野でもありますので,問に解説動画をつけています!
・像(Image)と核(Kernel)とはなにか理解すること
・像(Image)と核(Kernel)の基底と次元を求めることできるようになること
演習問題解説動画(演習問題はこの記事の”問”のことです)
線形写像に対応する行列
まず,像(Image)と核(Kernel)を求めるために線形写像に対応する行列についてみていきましょう.
線形写像に対応する行列
線形写像\( f:\mathbb{R}^n \rightarrow \mathbb{R}^m \)が与えられたとき,
\( f(\mathbf{x}) = A\mathbf{x} \)となる(n,m)型行列\( A \)が存在する.
この行列\( A \)を線形写像\( f \)に対応する行列という.
実際に例題を解いて行列を求めることができることが大切なので例題を通して理解していくことにしましょう.
例題:線形写像に対応する行列
次の線形写像\( f:\mathbb{R}^2 \rightarrow \mathbb{R}^3 \)
に対応する行列\( A \)を求めよ
\( f(\begin{pmatrix} x_1
\\x_2 \end{pmatrix} ) = \begin{pmatrix} x_1 + x_2
\\2x_1
\\3x_2 \end{pmatrix} \)
[例題:線形写像に対応する行列]
右辺は、\( \begin{pmatrix} x_1 \\x_2 \end{pmatrix} = \begin{pmatrix} x_1 + x_2 \\2x_1
\\3x_2 \end{pmatrix} = \begin{pmatrix} 1 & 1\\ 2 & 0\\0 & 3 \end{pmatrix} \)
と表現できるので、
\( A = \begin{pmatrix} 1&1\\2&0\\0&3 \end{pmatrix} \) ■
この,線形写像に対応する行列は後に像(Image)と核(Kernel)を計算する際に使用します.
では,冒頭から出てきている像(Image)と核(Kernel)とはいったい何なのか
定義することにしましょう.
像(Image)と核(Kernel)
線形写像\( f:V \rightarrow V^{\prime} \)に対して
・\( f \)による\( V \)の像
\( f(V) = \left\{f(v)|\pmb{v} \in V\right\} \)
を\( \mathrm{Im}f \)で表し,\( f \)の像という.
・\( V^{\prime} \)の零ベクトルの逆像
\( f^{-1}(\mathbf{0}) = \left\{\mathbf{x} \in V | f(\mathbf{x}) = \mathbf{0}\right\} \)
を\( \mathrm{ker}{f} \)と表し,fの核という.
もし,像とか逆像ってなんだっけという方がいれば
「像と逆像」の記事を参考にしてください.
それでは,定義について考えていきましょう.
像(Image)に関しては像の定義そのまんまです.
理解の助けになるように図をつけておきます.
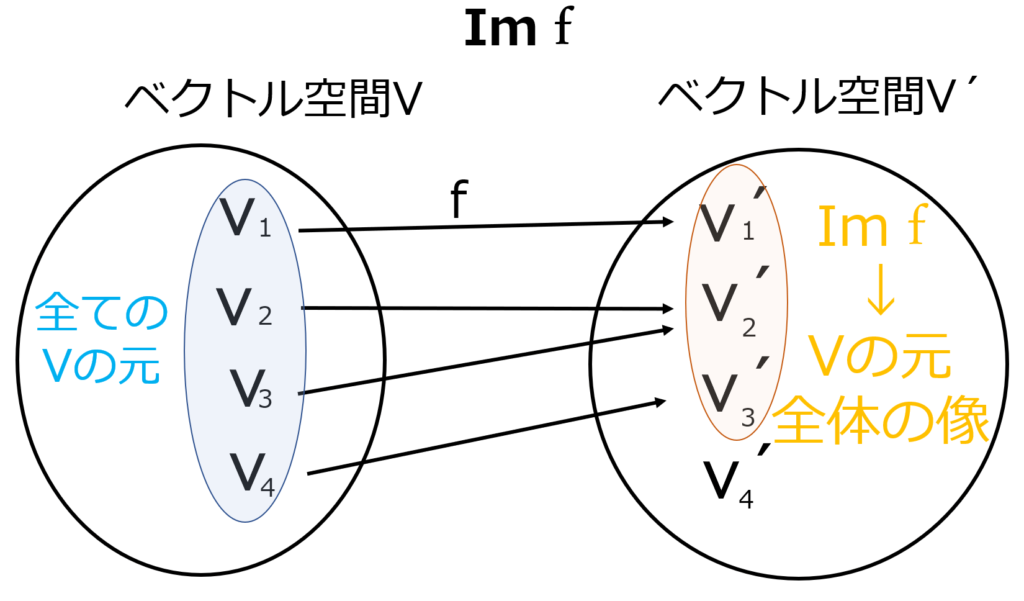

次に核(kernel)です.
kernelは\( V^{\prime} \)の零ベクトルの逆像ですから図で表すと
以下のようになります.
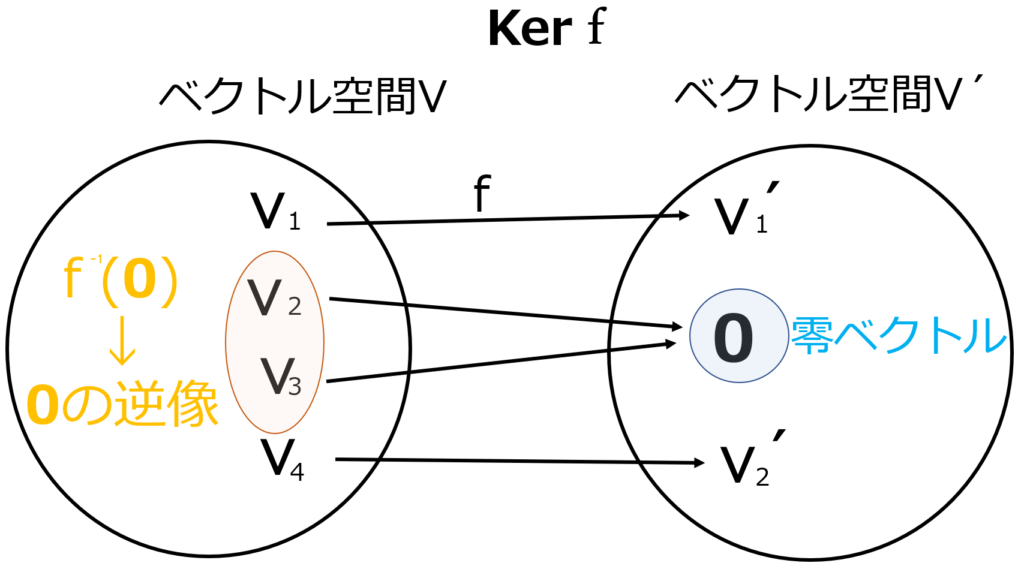

このkernelについては誤解している人が多いように思います.
零ベクトルの逆像ということをしっかりと頭に入れておきましょう.
それでは,ここからは試験でも頻出の像と核の基底と次元を求めていきましょう
像と核の基底と次元
像と核の基底と次元を求めるにあたって,
必要となる次元公式を先に定義します.
次元公式
\( V,V^{\prime} \)をベクトル空間,線形写像\( f:V \rightarrow V^{\prime} \)とするとき
\( \mathrm{dim}V = \mathrm{dim} \mathrm{Im}f + \mathrm{dim}\mathrm{ker}f \)
ではこの次元公式を用いて実際に例題を解いていきましょう.
例題は解答を詳しく書いています.
初めてだと解法に戸惑うかもしれませんが例題に沿って解いて問で力試しをするとよいでしょう.
例題:像と核
次の写像\( f:\mathbb{R}^3 \rightarrow \mathbb{R}^3 \)の像と核の次元と基底を一組ずつ求めよ.
\( f(\begin{pmatrix} x_1
\\x_2
\\x_3\end{pmatrix} ) = \left(\begin{array}{ccc}x_1 + x_2 + 3x_3\\x_1 + 2x_2 + 2x_3\\-x_1 – x_2 – 3x_3\end{array}\right) \)




例題中の基底を求める部分がよくわからない方は
「基底と次元」内の「定理:数ベクトル空間の基底」を参照してください.
今回は一次独立であることを用いています
それでは,この例題を参考にして問を解いてみることにしましょう!
問:像と核
次の写像\( f:\mathbb{R}^3 \rightarrow \mathbb{R}^3 \)の像と核の次元と基底を一組ずつ求めよ.
\( f ( \begin{pmatrix} x_1\\x_2\\x_3\end{pmatrix} )= \left(\begin{array}{ccc}x_1 + 3x_2 – x_3\\2x_1 + 7x_2\\-x_1 – 4x_2 – x_3\end{array}\right) \)


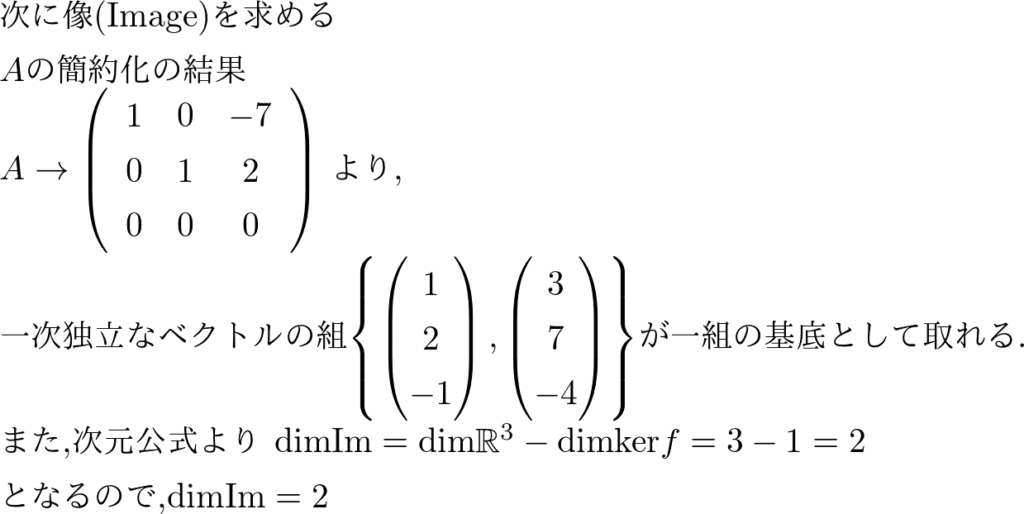
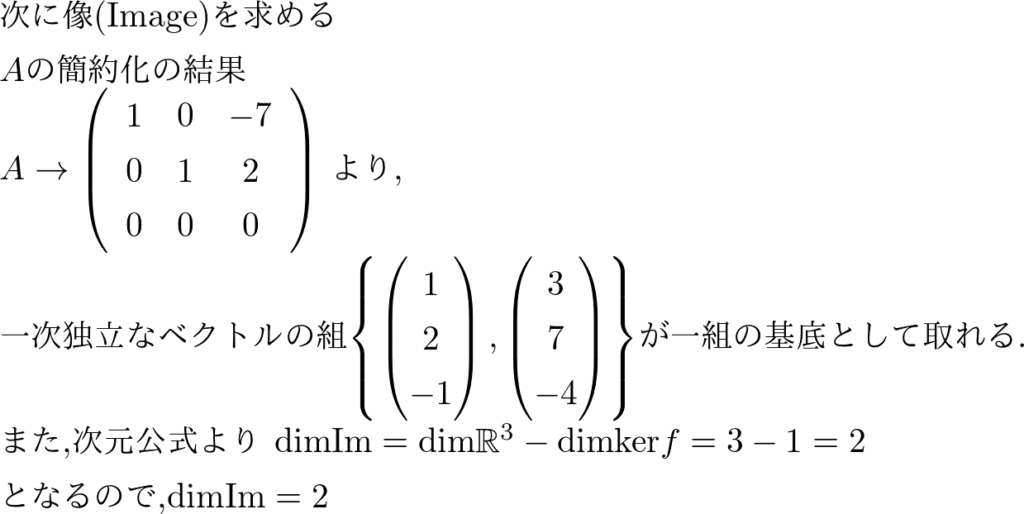
以上が、「像(Image)と核(Kernel)」です.
この単元は試験に頻出ですが苦手な方が多いです.
何度も復習してぜひ自分のものにしてしまいましょう!
それでは,まとめに入ります!
「像(Image)と核(Kernel)」まとめ
線形写像\( f:V \rightarrow V^{\prime} \)の像と核とは
・\( f \)による\( V \)の像
\( f(V) = \left\{f(V)|\pmb{v} \in V\right\} \)
を\( \mathrm{Im}f \)で表す.
・\( V^{\prime} \)の零ベクトルの逆像
\( f^{-1}(\mathbf{0}) = \left\{\mathbf{x} \in V | f(\mathbf{x}) = \mathbf{0}\right\} \)
を\( \mathrm{ker}{f} \)と表す.
入門線形代数記事一覧は「入門線形代数」




