「ベクトルの内積」では,ベクトル同士の掛け算についてみていきましょう!
ベクトル同士の掛け算はただ掛け算を行うだけではなく
ベクトルの方向も気にします(下で出てくるなす角のことです.)
・ベクトルの内積が計算できるようになる
ベクトルの内積
まずは.ベクトルの内積を定義するためにベクトルのなす角というものを定義しましょう.
ベクトルのなす角
零ベクトルではない二つのベクトル\( \mathbf{a} = \vec{OA},\mathbf{b} = \vec{OB}\)に対して\( \angle{AOB} = \theta(0 \leq \theta \geq 180^\circ)\)とする.
このとき,\( \theta\)を\( \mathbf{a}\)と\( \mathbf{b}\)のなす角という.
特に,\( \theta = 90^\circ\)のとき,\( \mathbf{a}\)と\( \mathbf{b}\)は直交するといい,
\( \mathbf{a} \perp \mathbf{b}\)とかく.
このベクトルのなす角について図にしてみましょう.
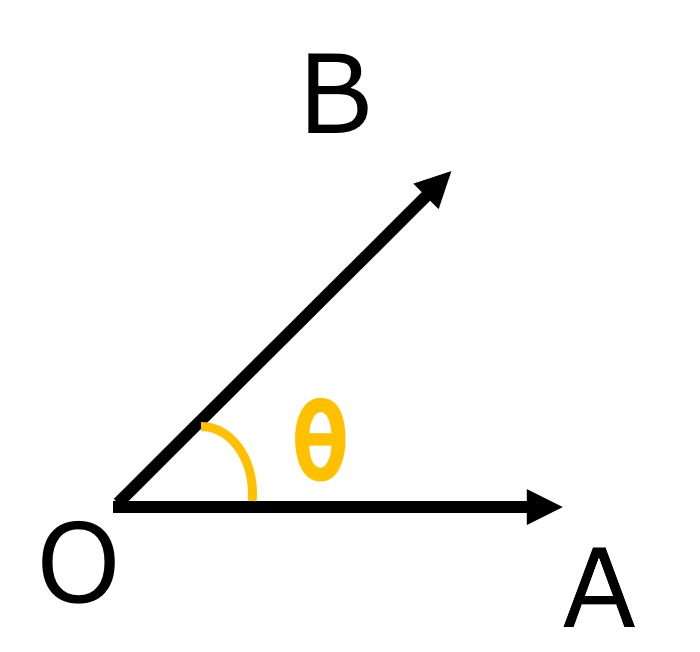
このベクトル通しで挟まれている部分の角度がなす角です.
定義にも書いてありますがこのなす角は\( \theta(0 \leq \theta \geq 180^\circ)\)で
表します.
では,このなす角を用いてベクトルの内積を定義しましょう!
ベクトルの内積
二つの零でないベクトル\( \mathbf{a}, \mathbf{b}\)に対して
\( \mathbf{a}\)と\( \mathbf{b}\)のなす角を\( \theta\)とすると
\( \mathbf{a}\)と\( \mathbf{b}\)の内積は各ベクトルの大きさを用いて
\( (\mathbf{a},\mathbf{b}) = \|\mathbf{a}\| \|\mathbf{b}\| \mathbf{cos}\theta\)となる.
ベクトルの内積については\( (\mathbf{a},\mathbf{b})\)以外にも
\( \mathbf{a}\cdot \mathbf{b}\)や\( <\mathbf{a},\mathbf{b}>\)といった表記もあります.
\( (\mathbf{a},\mathbf{b})\)という表記を使うときに注意していただきたいのは,
ベクトルの内積は”(「ベクトル」,「ベクトル」)”という形であらわします.
これを成分表示と間違えないように気を付けてください
”(「成分」,「成分」)”→ベクトルの成分表示
”(「ベクトル」,「ベクトル」)”→ベクトルの内積
となります.
このベクトルの内積を用いて一つ有名な性質を例として紹介します
直交するベクトルの内積
二つの零でないベクトル\( \mathbf{a}\),\( \mathbf{b}\)に対して
\( \mathbf{a}, \mathbf{b}\)が直交するとき
内積\( \mathbf{a}, \mathbf{b}\)は0となる.
このことを内積の定義から確認してみましょう

この直交するとき内積0というのは有名ですからぜひおさえておきましょう.
それでは,実際に内積を求める問題を解いてみることにしましょう!
例題:ベクトルの内積
零ベクトルでなく平行でない二つのベクトル\( \mathbf{a},\mathbf{b}\)が
\( \|\mathbf{a}\| = 2, \| \mathbf{b} \| = 2\)なす角\( \theta = 60^{\circ}\)のとき,
\( \mathbf{a},\mathbf{b}\)の内積\( \mathbf{a} \cdot \mathbf{b}\)を求めよ

最後に問をつけておきます.
問:ベクトルの内積
零ベクトルでなく平行でない二つのベクトル\( \mathbf{a},\mathbf{b}\)に対して次の条件の時の内積\( \mathbf{a} \cdot \mathbf{b}\)を求めよ
(1)\( \| \mathbf{a}\| = 4, \| \mathbf{b} \| = 3\)なす角\( \theta = 120^{\circ}\)
(2)\( \| \mathbf{a}\| = 2, \| \mathbf{b} \| = 5\)なす角\( \theta = 90^{\circ}\)
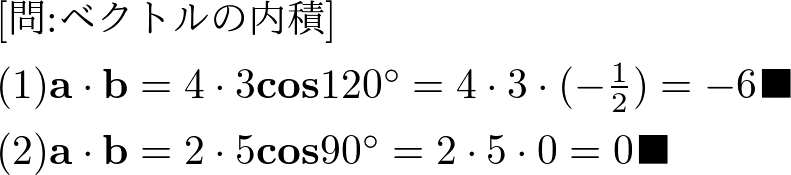
では,最後に内積に成り立つ基本的な性質を紹介します!
定理:ベクトルの内積の基本性質
3つのベクトル\( \mathbf{a},\mathbf{b},\mathbf{c}\)と\( k\in\mathbb{R}\)に対して
(1)\( (\mathbf{a},\mathbf{b}) = (\mathbf{b},\mathbf{a})\)
(2)\( ( (\mathbf{a} + \mathbf{b}),\mathbf{c} )= (\mathbf{a},\mathbf{c}) + (\mathbf{b},\mathbf{c})\)
(3)\( ( (k\mathbf{a}),\mathbf{b} ) = k(\mathbf{a},\mathbf{b}) = (\mathbf{a},(k\mathbf{b}))\)
(4)\( \mathbf{a}\cdot\mathbf{a} = \|\mathbf{a}\|^2\)
(5)\( \mathbf{a}\neq0,\mathbf{b}\neq0,\mathbf{a}\perp\mathbf{b} \Rightarrow \mathbf{a}\cdot\mathbf{b} = 0\)
この基本的な性質を使って成分表示されたベクトルの内積を計算したりしますが,
それは別の記事にまとめることにします!
それではまとめに入ります!
「ベクトルの内積」まとめ
・ベクトルの内積は\( (\mathbf{a},\mathbf{b}) = \|\mathbf{a}\| \|\mathbf{b}\| \mathbf{cos}\theta\)

