「ベクトルとは?」では,ベクトルという概念を数学的に定義します.
このベクトルはタイトルにもあるベクトル空間のスタートとなり今後ずっと議論していく対象でもありますので,しっかりマスターしてしまいましょう!
・ベクトルとはなにか理解すること.
・ベクトルが等しいとは何か理解すること
目次
- ベクトルとは?
- ベクトル
- ベクトルの大きさ
- 平行なベクトル
- ベクトルの相等
- 「ベクトルとは?」まとめ
ベクトルとは?
平面または空間において2点A,Bに向きを定めた線分のことを有向線分という.
特に,点Aから点Bに向かう有向線分ABを
Aを始点,Bを終点とするベクトルといい,\( \vec{AB}\)とあらわす.
始点と終点とは,ベクトルのスタート地点とゴール地点です.
すなわち,\( \vec{AB}\)はAをスタートしBでゴールするベクトルということです.
また,ベクトルを表現する際に太文字を用いて
\( \mathbf{a}\)(\( =\vec{a}\))を用いて表しますので,この表現方法を併せて
おさえておきましょう!
では,次にベクトルに大きさという概念を定義しましょう.
ベクトルの大きさとは
ベクトル\( \vec{AB}\)を線分ABの長さで表したものであり
\( \|\vec{AB}\|\)とかく.
ベクトルとその大きさについてここまでのことを図にまとめましょう!
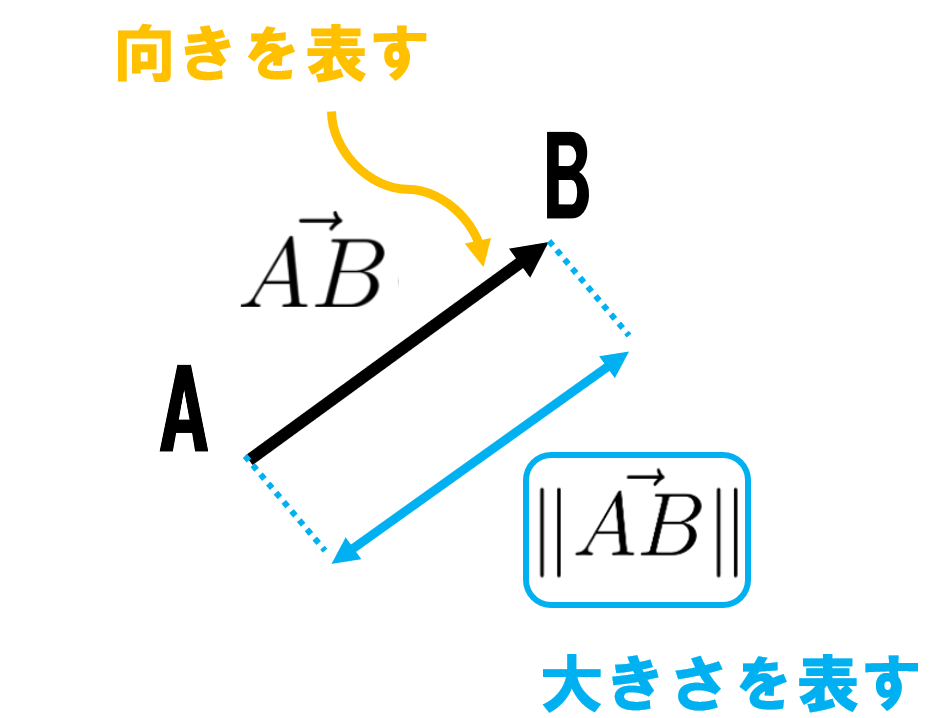
この図のように有向線分とその長さでベクトルと大きさを表現します!
では,ベクトル同士の相等を言うために必要なベクトルの平行を定義しましょう!
2つのベクトル\( \vec{AB}\)と\( \vec{CD}\)の
向きが同じもしくは反対向きの時,\( \vec{AB}\)と\( \vec{CD}\)は平行
といい,\( \vec{AB}\parallel \vec{CD}\)で表す.
平行に関しては向きが反対でも問題ありません.
詳しい話は成分表示されたベクトルの話をしてからのほうがわかりやすいと思いますので,
今回はこのあたりにしておきましょう.
では,最後にベクトルの相等を定義してしまいます!
2つのベクトル\( \vec{AB}\)と\( \vec{CD}\)に対して,
向きが同じでかつ大きさが同じとき,すなわち
\( \|\vec{AB}\| = \|\vec{CD}\|, \vec{AB}\parallel \vec{CD}\)のとき
ベクトル\( \vec{AB}\)と\( \vec{CD}\)は等しいといい,
\( \vec{AB} = \vec{CD}\)とかく.
まず,図を使いイメージをつかみましょう!
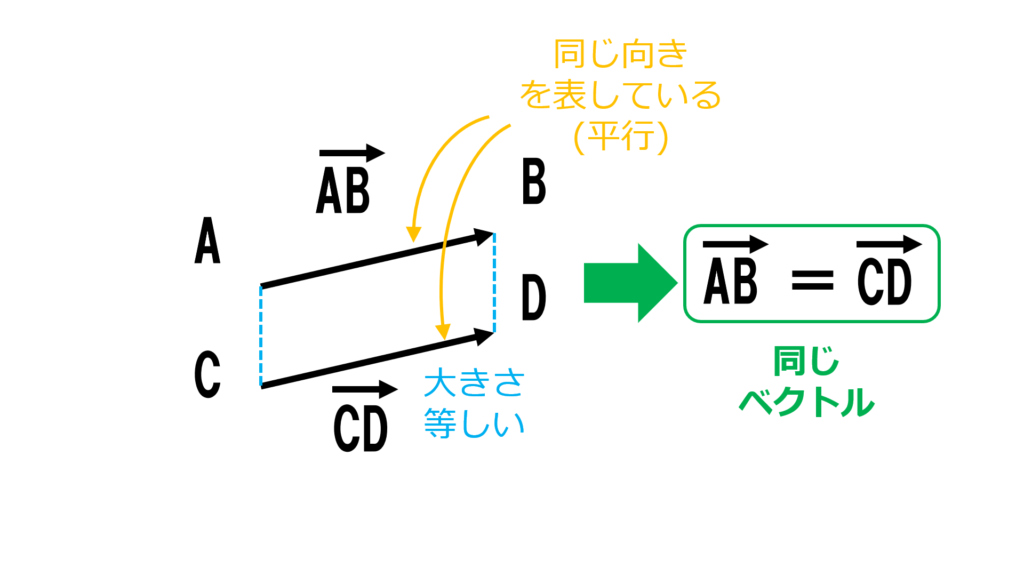
このようにベクトルの 相等は向きと大きさで定義しており位置については言及していないです.
一見,\( \vec{AB}\)と\( \vec{CD}\)は別のものに見えてもこの平面(空間)上
では同じものと捉えます.
以上が「ベクトルとは?」という話です.
向きと大きさで定義された少し新しい概念です笑
ベクトル空間ではこのベクトルをさらに一般化して考えます!
以降のベクトル空間もぜひ楽しんでください!
それではまとめに入ります!
「ベクトルとは?」まとめ
・点Aから点Bに向かう有向線分ABをAを始点,Bを終点とするベクトルという
・ベクトルが等しいとは,2つのベクトルの向きが同じでかつ大きさが同じ

