表現行列は3記事に分けて説明していきます.「表現行列①」は表現行列の1記事目です.
「表現行列①」では,表現行列の定義とその定義に忠実に表現行列を計算できるようになっていこうと思います!!
・表現行列とは何か理解すること
・表現行列を計算できるようになること.
表現行列
表現行列とはベクトル空間上の基底を用いて線形写像を表していくことです.
といっても実際にどうなるのか定義していきましょう.
表現行列
ベクトル空間\(V,V^{\prime}\)のそれぞれの基底の一組を
\( \left\{ \mathbf{v_1},\mathbf{v_2},\cdots,\mathbf{v_n} \right\} \) ,\( \left\{\mathbf{v_1}^{\prime},\mathbf{v_2}^{\prime},\cdots,\mathbf{v_m}^{\prime}\right\} \) とする.
線形写像\(f:\mathbf{V}\rightarrow \mathbf{V}^{\prime}\)に対して
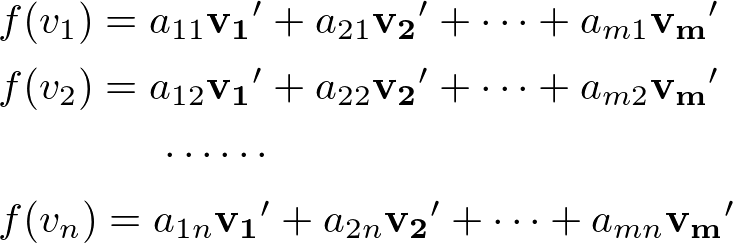
を満たすとする.
このとき,右辺の係数を並べた行列

のことを,
\(f\)の基底\(\left\{\mathbf{v_1},\mathbf{v_2},\cdots,\mathbf{v_n}\right\}\),\( \left\{\mathbf{v_1}^{\prime},\mathbf{v_2}^{\prime},\cdots,\mathbf{v_m}^{\prime}\right\} \)
に関する表現行列という.
何となく基底を用いて線形写像を表現しているのだろうなということはわかっていただけるかと思います.
では,この定義を用いて実際に表現行列を求めていくことにしましょう.
定義に沿って例題を解いていくことにします.
例題:表現行列
線形写像\(f:\mathbb{R}^3 \rightarrow \mathbb{R}^2\),\(\begin{pmatrix} x_1
\\x_2
\\x_3\end{pmatrix} \longmapsto \left(\begin{array}{ccc}x_1 + 2x_2 – x_3
\\2x_1 – x_2 + x_3 \end{array}\right) \)
の次の基底に関する表現行列\(B\)を求めよ.
\(\mathbb{R}^3 \)の基底:\(\left\{ \begin{pmatrix} 1
\\0
\\0\end{pmatrix},\begin{pmatrix} 1
\\2
\\-1\end{pmatrix},\begin{pmatrix} -1
\\0
\\1\end{pmatrix} \right\}\)
\( \mathbb{R}^2 \)の基底:\( \left\{ \begin{pmatrix} 2
\\-1\end{pmatrix},\begin{pmatrix} -1
\\1\end{pmatrix} \right\} \)

以上の例題から表現行列を求めるstepをまとめておきましょう.
表現行列を求めるstep
(step1)
\(f(v_n) = a_{1n}\mathbf{v_1}^{\prime} + a_{2n}\mathbf{v_2}^{\prime} + \cdots +a_{nm}\mathbf{v_m}^{\prime} \)
を満たす係数(\(a_{1n},a_{2n},\cdots,a_{mn}\) )を求める.
(step2)求めた係数を並べた行列

を作る.
では,例題とstepを用いて力試しとして問を解いていくことにしましょう
問:表現行列
線形写像\( f:\mathbb{R}^2\rightarrow\mathbb{R}^3\) ,\( \left(\begin{array}{ccc}x_1\\x_2\end{array}\right) \longmapsto \left(\begin{array}{cc}-2x_1- 2x_2\\x_1\\x_2 \end{array}\right)\)
の次の基底に関する表現行列\( B\) を求めよ.
\( \mathbb{R}^2\) の基底:\( \left\{ \begin{pmatrix} -2
\\1\end{pmatrix},\begin{pmatrix} -2
\\2\end{pmatrix} \right\}\),
\( \mathbb{R}^3\) の基底:\( \left\{ \begin{pmatrix} 1
\\-1
\\0\end{pmatrix},\begin{pmatrix} 0
\\2
\\2\end{pmatrix},\begin{pmatrix} 2
\\0
\\1\end{pmatrix} \right\}\)

以上が,「表現行列①」です.
冒頭にも話しましたが表現行列はこの後「表現行列②」「表現行列➂」と続きます.
「表現行列②」では定義からではなく公式のようなものを扱って表現行列を求めていきます.
「表現行列➂」では②を利用して線形変換という特別な線形写像に対して公式を扱います.
どれも試験等で必須なうえ苦手な人が多い単元なので,しっかり復習してマスターしましょう
それでは、まとめに入ります!
「表現行列①」まとめ
・表現行列とは,ベクトル空間(V,V^{\prime})のそれぞれの基底の一組を用いて,線形写像を表現したもの.
・表現行列を求めるstepは
(step1)
\(f(v_n) = a_{1n}\mathbf{v_1}^{\prime} + a_{2n}\mathbf{v_2}^{\prime} + \cdots +a_{nm}\mathbf{v_m}^{\prime} \)
を満たす係数(\(a_{1n},a_{2n},\cdots,a_{mn}\) )を求める.
(step2)求めた係数を並べた行列をつくる.
入門線形代数記事一覧は「入門線形代数」

