「部分空間」では,ベクトル空間の部分集合について議論していこうと思います!
部分空間かどうか判定できるようになることは今後の学習で大切になってきますので
ぜひともしっかりとマスターしてしまいましょう!
・部分空間かどうか判定できるようになること
この記事の問には解説動画が付いています!
部分空間
部分空間
\( \mathbb{K} \)上のベクトル空間\( V \)の部分集合\( W \)が以下の3つの条件を満たすとき\( W \)を\( V \)の部分空間という。
(S-0)\( \mathbf{0} \in W \)
(S-1)\( \mathbf{w_1,w_2} \in W \Rightarrow \mathbf{w_1} + \mathbf{w_2} \in W \)
(S-2)\(\mathbf{w} \in W,k \in \mathbb{K} \Rightarrow k\mathbf{w} \in W \)
この定義のポイントは2つあります。
まず一つ目は零ベクトルが部分集合\( W \)に含まれていることです.
この条件がないと定義4-1の零ベクトルの存在を保証できなくなるので、忘れがちな条件ですがしっかり頭に入れておきましょう.
もう一つのポイントは(S-1)と(S-2)どこかで見たことありませんか?
これは定義4-1の(和に関する性質)と(スカラー倍に関する性質)を部分集合でも満たすということです.
なのでベクトル空間の時にように8つも調べなくてもで和とスカラー倍に関する性質を
満たしていれば,\( W \)は部分空間であると示せます!
問:部分空間
(1) \( \mathbb{R} \)上のベクトル空間\( \mathbb{R}^3 \)の部分集合
\( W_1 = \left\{ \begin{pmatrix} x \\y
\\z \end{pmatrix} \in \mathbb{R}^3 \mid x + y + z = 0 \right\} \)
\( W_2 = \left\{ \begin{pmatrix} x
\\y
\\z \end{pmatrix} \in \mathbb{R}^3 \mid x + y + z = 1 \right\} \)
は、\( \mathbb{R}^3 \)の部分空間であるか?
(2) \( \mathbb{R} \)上のベクトル空間\( \mathbb{R}^4 \)の部分集合
\( W_1 = \left\{ \begin{pmatrix} x\\y\\z\\w \end{pmatrix} \in \mathbb{R}^4 \mid x = y , z = w \right\} \)
\( W_2 = \left\{ \begin{pmatrix} x\\y\\z\\w \end{pmatrix} \in \mathbb{R}^4 \mid x + y + z + w^2= 0 \right\} \)
は、\( \mathbb{R}^4 \)の部分空間であるか?
部分空間かどうか確認するためには、定義4-2の(S-0)~(S-2)の内容を確認すればいいですので\( W_1,W_2 \)のそれぞれに対して(S-0)~(S-2)を確認していきましょう.
<例題の解答>

\( W_1 \)に関しては確かに定義4-2の(S-0)~(S-2)が確認できましたので部分空間といえますね.
では、同じように\( W_2 \)は部分空間になるのか確認してみることにしましょう.
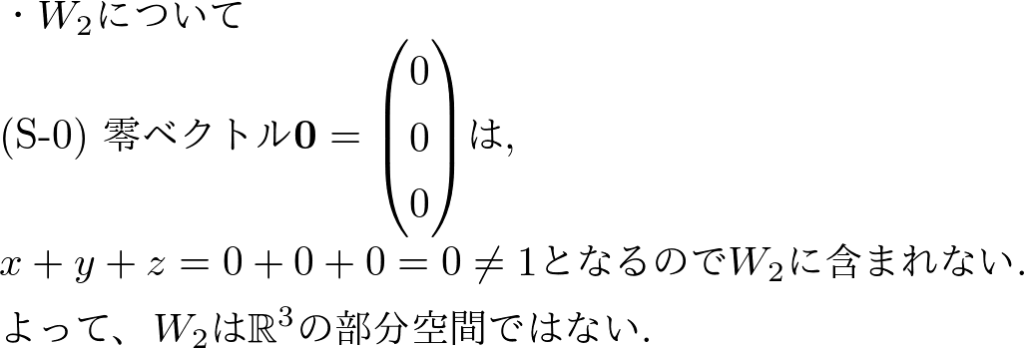
少し拍子抜けかもしれませんが問題によっては(S-1)と(S-2)はみたすのに(S-0)は満たさないため部分空間ではないという問題があります.
そういった問題の為に改めてちゃんと(S-0)というのがあったと
インプットしてほしいという願いを込めてこの例題を付けました.
では,少しレベルを上げて数ベクトル空間\(\mathbb{R}^4\)の部分空間
を扱っていきましょう!
問:部分空間
ベクトル空間\( \mathbb{R}^4 \)の部分集合\( W_1,W_2 \)
\( W_1 = \left\{ \left. \begin{pmatrix} x\\y\\z\\w \end{pmatrix} \in \mathbb{R}^4 \right| x = y , z = w \right\} \)
\( W_2 = \left\{ \left. \begin{pmatrix} x\\y\\z\\w \end{pmatrix} \in \mathbb{R}^4 \right| x + y + z + w^2= 0 \right\} \)
は、\( \mathbb{R}^4 \)の部分空間であるか?

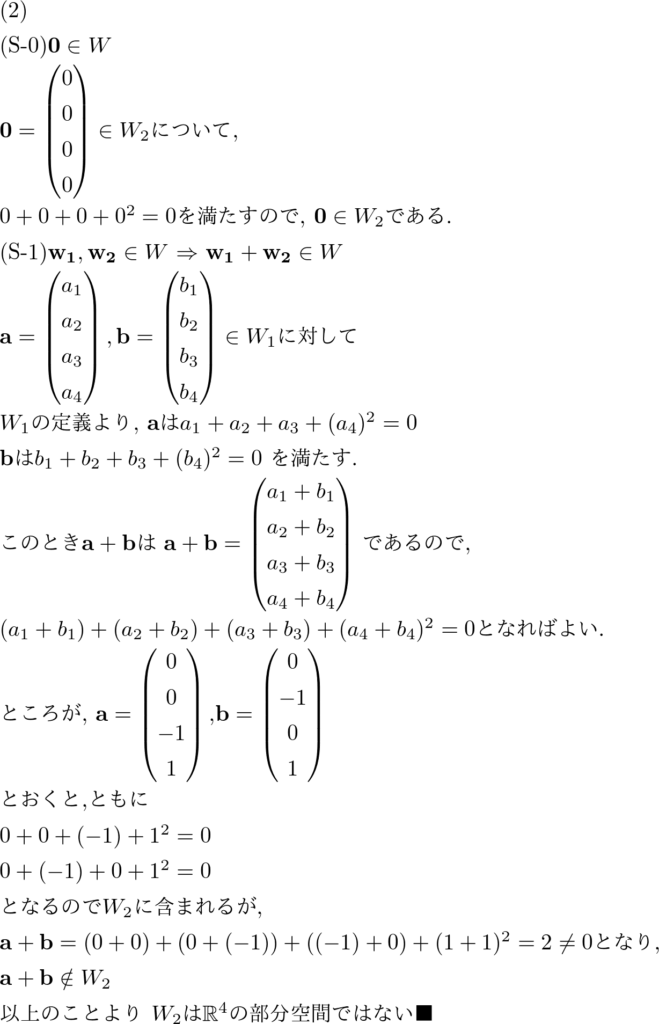
以上が「部分空間」という話しでした.
部分空間かどうか判別する問題は定期テスト等の試験で頻出の問題になりますので
今回挙げた例題と問を通してしっかりと復習しておくとよいでしょう!
それではまとめに入ります!
「部分空間」まとめ
・部分空間とは(S-0)~(S-2)を満たす,ベクトル空間の部分集合のこと.
入門線形代数記事一覧は「入門線形代数」

