今回は, 行列の「行基本変形」と呼ばれる操作について解説します.
行基本変形を行うことで行列をシンプルな形に変形することができます.
また, この操作は連立一次方程式を解くことや, その先の単元でもとても大切になるので, しっかりマスターしましょう!
・行列の行基本変形ができるようになる!
行列の行基本変形
先に具体例を見ます.
「拡大行列と拡大係数行列」で使った連立一次方程式\( (*) \)を使って基本変形をみていきます.
まず, 連立一次方程式を加減法を使って解きます.
(後で行列と見比べるので, 敢えて0を書いていきます.)
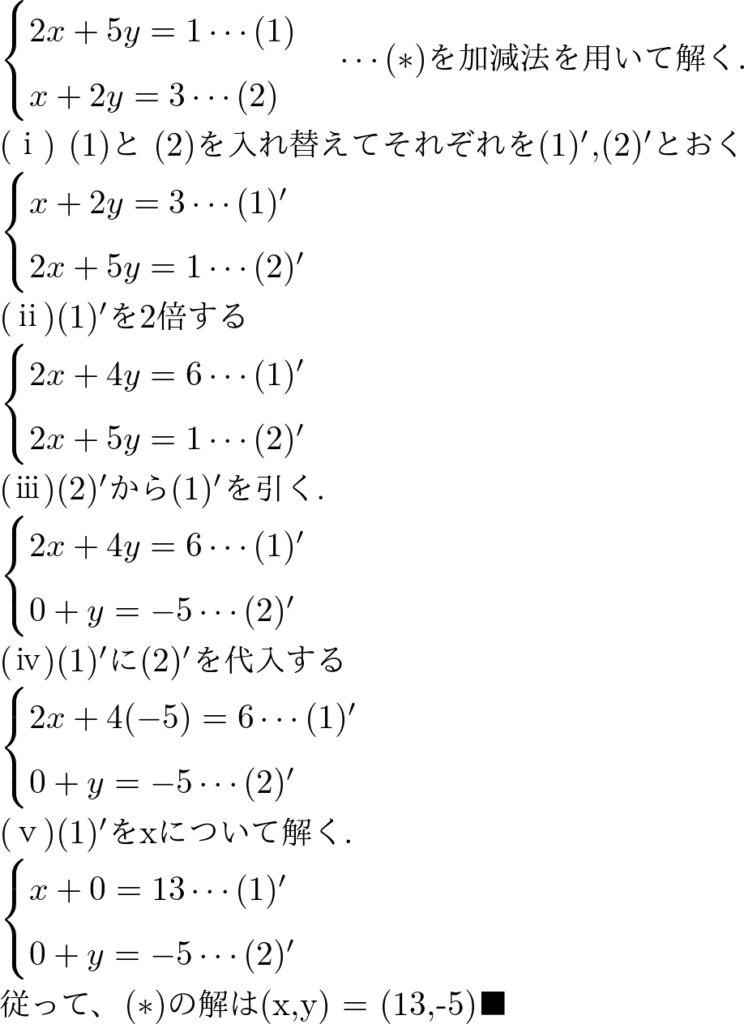
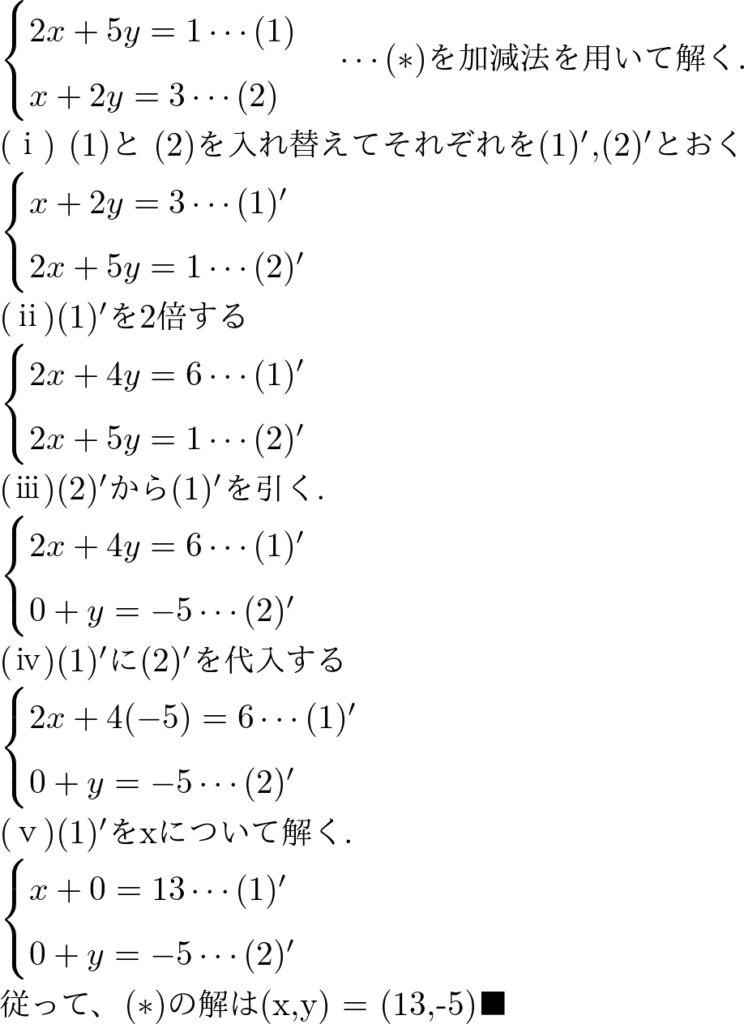
このような手順を踏んで, 中学生の頃から連立一次方程式の解を求めましたね.
連立一次方程式を解く際, 以下の3パターンの操作が行われます.
(Ⅰ)2つの式を入れ替える.
(Ⅱ)ある式を何倍かする.
(Ⅲ)1つの式に, ほかの式の何倍かを加える.
この(Ⅰ)~(Ⅲ)を, 行列について行ってみます.


このように, 行列でも連立一次方程式の時と同じように変形が可能です.
行列に対して実際に行った変形をまとめると, 以下の3パターンの変形になります.
(Ⅰ)2つの行を入れ替える.
(Ⅱ)ある行を何倍かする.
(Ⅲ)1つの行に, ほかの行の何倍かを加える.
式の操作と, 行の操作が対応していることがわかりますね.
( I ), ( II ), (Ⅲ)の変形を行基本変形といいます.
(行基本変形を用いて連立一次方程式を解く方法を掃き出し法といいますが,
掃き出し法は別記事「掃き出し法」でまとめています)
行列の行基本変形
行列の行基本変形とは以下の3つの操作を行列に対して行うことである.
(Ⅰ)2つの行を入れ替える.
(Ⅱ)ある行を何倍かする.
(Ⅲ)1つの行に, ほかの行の何倍かを加える.
この先, 行基本変形による行列の変形をたくさんするので, 3つの操作はしっかりと覚えましょう!
ここで, 一点注意です.
行基本変形を行う際は, 変形前と変形後の行列を「→」で結びましょう!
例えば, 上の具体例の(ⅰ)の変形は以下のように書かれます.
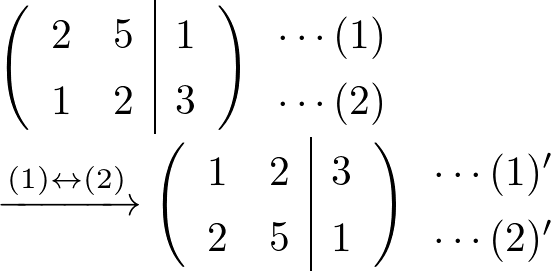

間違っても=で結んではいけません!!
「→」以外にも色々な結び方がありますが, ここでは「→」を使って書き進めていきます.
それでは, 行基本変形の練習をしましょう!
問:行列の行基本変形
次の行列を行基本変形を用いて, 単位行列に変形せよ.
(1)
\( \left(\begin{array}{cc}
2 & -3 \\
-1 & 2
\end{array}\right) \)
(2)
\( \left(\begin{array}{ccc}
-1 & 2 & -1 \\
1 & 2 & 2 \\
3 & 2 & 1
\end{array}\right) \)
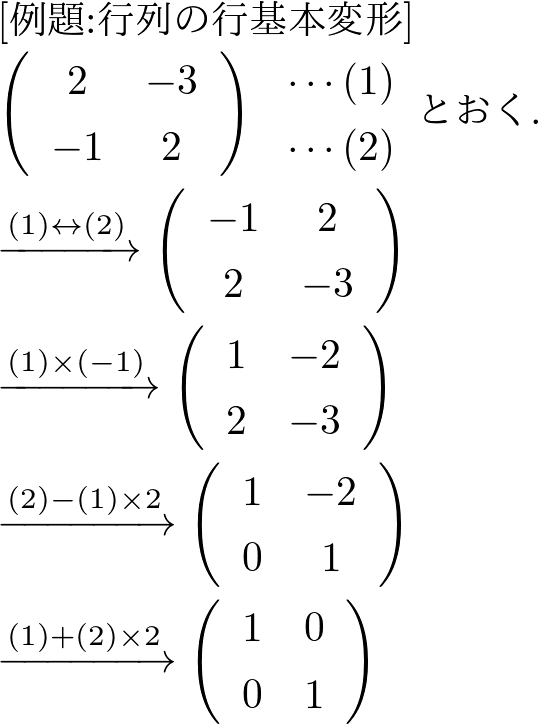
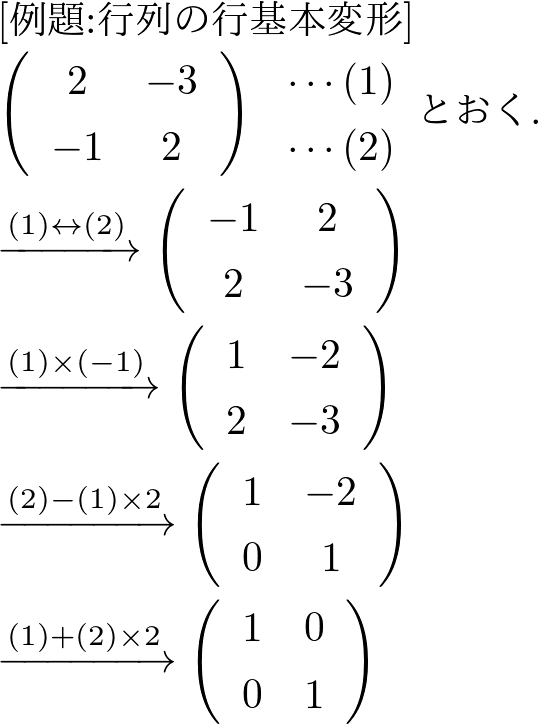


以上の変形により単位行列に変形できた■
このようにして基本変形の操作を行います.
冒頭にも言いましたが, 基本変形は今後行列を扱うための基本であり, 様々なところで出てくるのでしっかりマスターしましょう!
それでは今回のまとめに入ります.
「行列の行基本変形」のまとめ
・行列の行基本変形とは行列に対して以下の3つの操作を行うことである.
(Ⅰ)2つの行を入れ替える.
(Ⅱ)ある行を何倍かする
(Ⅲ)1つの行に, ほかの行の何倍かを加える
入門線形代数記事一覧は「入門線形代数」


