「行列の簡約化」は連立一次方程式の解を求める方法である「掃き出し法」につながる内容です.
連立一次方程式を上手に解くためにも, 簡約化の内容をしっかりと抑えましょう!
・簡約行列を判断できるようになる.
・行列の簡約化ができるようになる.
簡約行列
簡約行列
まず, 簡約行列は以下のような行列です.
以下の条件を満たす階段行列を簡約行列という.
(ⅰ)主成分が全て1である.
(ⅱ)主成分を含む列では, 他の成分は全て 0 である.
階段行列の内容が怪しいと感じたら以下の記事で復習しましょう.
簡約行列のイメージを掴むために, 具体例を見ましょう!
例:簡約行列である行列
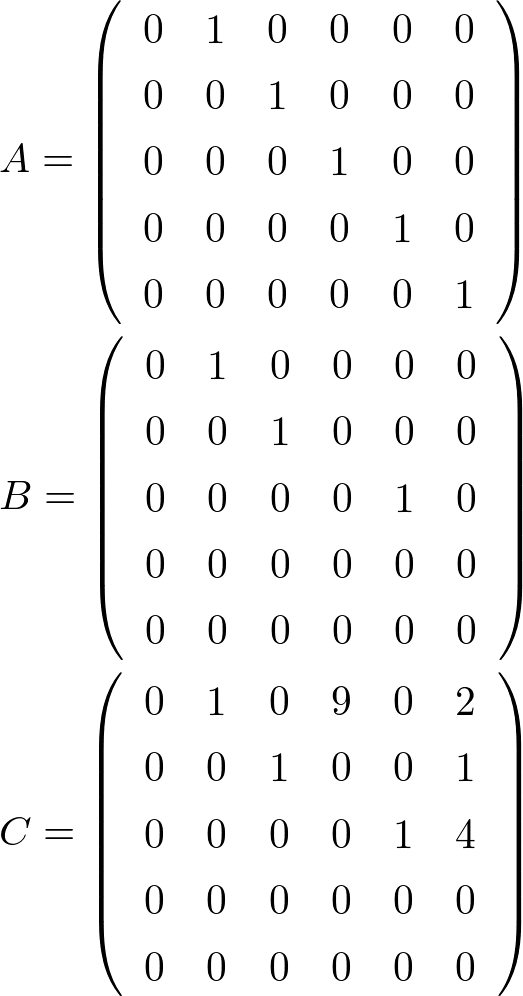
次の行列は全て簡約行列である.

<例の確認>
今回は, 簡約行列の例として\( A,B,C \)の3つの行列を例に挙げました.
1つずつ条件を満たしていることを確認していくことにしましょう.
・\( A \)について
まず, 前提として階段行列になっています.
条件(ⅰ)各行の主成分が1である. →これに関してもしっかり満たしています
条件(ⅱ)各行の主成分を含む列では, 他の列成分は全て0である.
1つずつ主成分を含む列を確認していくことにしましょう.
第1行目の主成分は第2列目にあります.
第2列目は第1行目以外すべて0なので条件を満たします.
第2行目の主成分は第3列目にあります.
第3列目は第2行目以外すべて0なので条件を満たします.
第3行目の主成分は第4列目にあります.
第4列目は第3行目以外すべて0なので条件を満たします.
第4行目の主成分は第5列目にあります.
第5列目は第4行目以外すべて0なので条件を満たします.
第5行目の主成分は第6列目にあります.
第6列目は第5行目以外すべて0なので条件を満たします.
よって, 条件(ⅱ)を満たすことも確認できました.
・\( B \)について
まず, 前提として階段行列になっています.
条件(ⅰ)各行の主成分が1である. →これに関してもしっかり満たしています
条件(ⅱ)各行の主成分を含む列では, 他の列成分は全て0である.
第1行目の主成分は第2列目にあります.
第2列目は第1行目以外すべて0なので条件を満たします.
第2行目の主成分は第3列目にあります.
第3列目は第2行目以外すべて0なので条件を満たします.
第3行目の主成分は第5列目にあります.
第5列目は第3行目以外すべて0なので条件を満たします.
よって, 条件(ⅱ)を満たすことも確認できました.
・\( C \)について
この行列を見たときに簡約行列なのだろうかと思う方もいるかもしれませんが, 実はしっかりすべての条件を満たしています. 確認してみましょう.
まず, 前提として階段行列になっています.
条件(ⅰ)各行の主成分が1である. →これに関してもしっかり満たしています
条件(ⅱ)各行の主成分を含む列では, 他の列成分は全て0である.
第1行目の主成分は第2列目にあります.
第2列目は第1行目以外すべて0なので条件を満たします.
第2行目の主成分は第3列目にあります.
第3列目は第2行目以外すべて0なので条件を満たします.
第3行目の主成分は第5列目にあります.
第5列目は第3行目以外すべて0なので条件を満たします.
よって, 条件(ⅱ)を満たすことも確認できました.
(1,4)成分や第6列目に色々ありますが, 主成分とは関係ないところなのでこの列に数字が入っていても問題ありません.
では, 逆に簡約行列ではない行列を見ていきましょう!
例:簡約行列でない行列
次の\( A,B \)は簡約行列ではない.
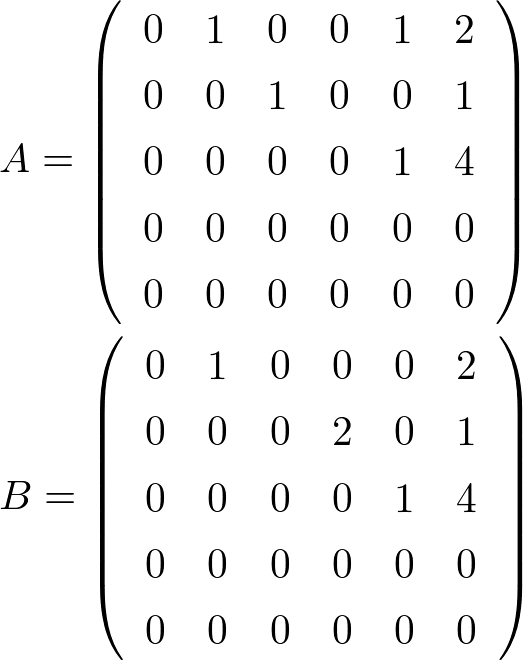

一見簡約行列に見えるかもしれませんが, この二つは簡約行列ではありません,
どこが条件に反してしまうのか確認していくことにしましょう.
<例の確認>
・\( A \)について
まず, 前提として階段行列になっています.
条件(ⅰ)各行の主成分が1である. →これに関してもしっかり満たしています
条件(ⅱ)各行の主成分を含む列では, 他の列成分は全て0である.
第3行目の主成分は第5列目にあります.
しかし, 第5列目は第3行目以外にも第一行目が0ではありません.
これは主成分以外が0であるという条件に反しているので, この行列は簡約行列ではありません.
・\( B \)について
まず, 前提として階段行列になっています.
条件(ⅰ)各行の主成分が1である. →これに関して第2行目が条件を満たしていません.
簡約行列が何かという話しはここまでにします.
次に, 行列を簡約化する方法について解説します.
行列の簡約化
行列の簡約化
行列\( A \)は行基本変形を繰り返すことで, 簡約行列が得られる.
この操作を, \( A \)の簡約化という.
簡約化について注意点があります.
簡約化された行列は, ただ一通りに定まります. これを簡約化の一意性といったりします.
要するに, どの手順で簡約化を行ったとしても, 最終的な結果は同じものになるということです.
では,実際に例を用いて行列の簡約化を行っていきましょう
問:行列の簡約化
次の行列\( A \), \( B \)を簡約化せよ.
\( A = \left(\begin{array}{cc}2 & 3
\\-1 & 2 \end{array} \right) \),
\( A = \left(\begin{array}{crl}1 & 1 & 4
\\-1 & 2& 2
\\3 & 1 & 2 \end{array} \right) \)
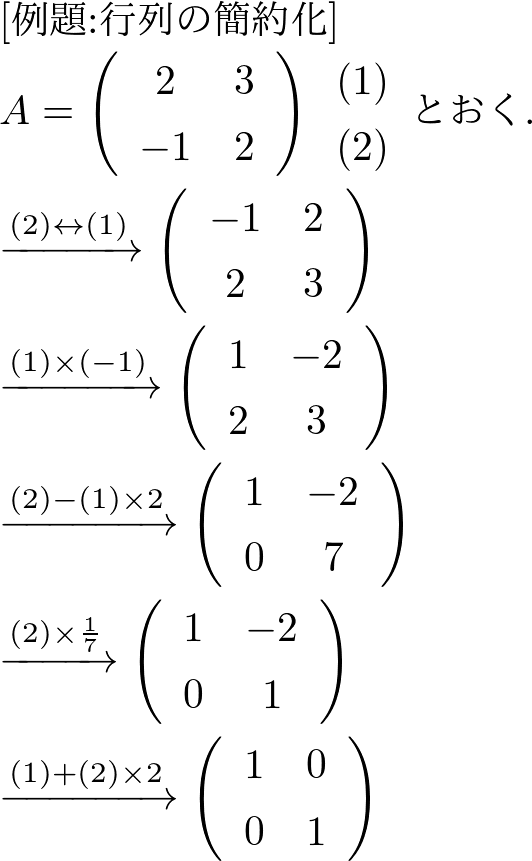
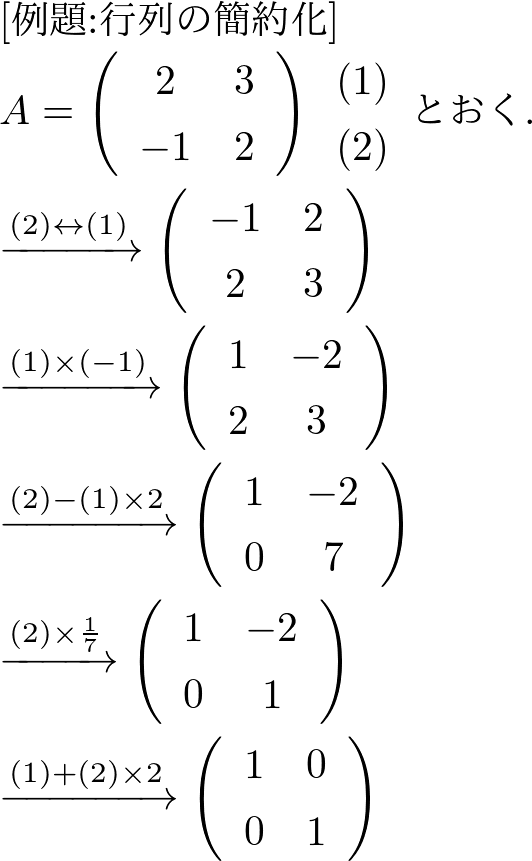


以上が「行列の簡約化」についてです.
長い道のりでしたが, ようやく連立一次方程式を解く準備が整いました.
次回は大本命である, 「連立一次方程式を解く」方法を解説します‼︎
これまでの内容をしっかり復習しておきましょう!
それではまとめに入ります.
「行列の簡約化」のまとめ
・簡約行列とは,
(ⅰ)各行の主成分が1であり,
(ⅱ)各行の主成分を含む列では, 他の列成分は全て 0 である
ような行列のこと.
・行列の簡約化とは,
基本変形を繰り返して, 簡約行列を得ること.
入門線形代数記事一覧は「入門線形代数」


