「いろいろな行列」では,単位行列や零行列のように特別に名前のついた行列がいくつかありますのでそのうちの
正方行列と転置行列を紹介します.
転置行列と単位行列について理解する
色々な行列
正方行列
(n,n)型行列、n×n型行列のことをn次正方行列という
正方行列とはその名の通り正方形の行列と考えても良いかと思います.
実際に行と列の大きさが等しいですので行列は正方形をしています.
実際にいくつか例を挙げて確認してみましょう
例:正方行列
以下の行列は3次正方行列である.
$$ \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 1 \\ 0 & 1 & 1\end{pmatrix}$$
<例の確認>
今回例に挙げた行列のサイズは3×3型行列なので3次正方行列です.
正方行列という言葉は今後頻出ですのでよく覚えておくとよいでしょう!
では,次に転置行列という行列を定義します.
転置行列
\( A = (a_{ij}) \)を(m,n)型行列とする.
\( A \)のできる(n,m)型行列のことをAの転置行列といい\( {}^t\!A \)とかく.
行と列を入れ替えるとは,
例えば\( a_{12} \)という成分に対して\( a_{21} \)を行と列を入れ替えた成分といい,
このようにしてすべての成分に対して行と列を入れ替えてできた行列の事を転置行列といいます.
さらに転置行列の定義を少し違う視点で見直してみることにします.
行列Aの転置行列\( ^{t}A \)は対角成分を基準にして対称に成分同士を交換させたものである.
とも言い換えることができます.
どういうことなのか図を使って確認していきましょう.
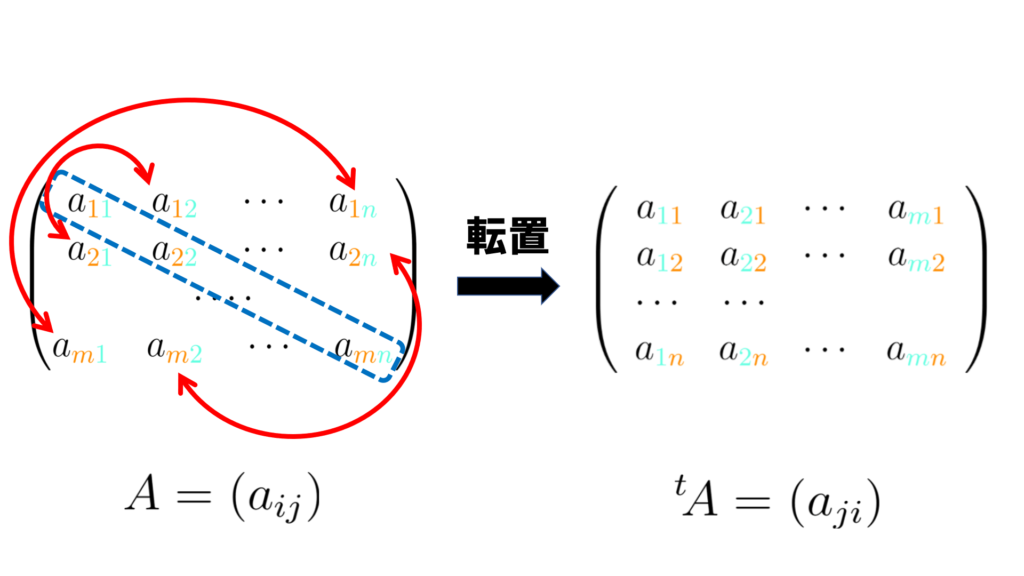
このように対角成分は動かさず、対面にある成分を交換させることで
転置行列は出来上がっています.
では、最後に転置行列について成り立つ性質を定理として紹介します.
定理:転置行列の性質
演算が定義された行列\( A,B \)と実数または複素数\( c \)に対して
以下のことが成り立つ.
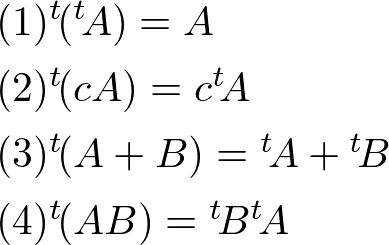
この定理のなかで特に間違いが多いのが(4)です.
この性質を間違えて\( {}^t\!(AB) = {}^t\!A{}^t\!B \)と覚えてしまっている人が多いです.
のちの計算に影響を及ぼしますので積の転置は積の順番を入れ替えることをしっかり押さえておいて下さい
ここで紹介した行列以外にも様々な行列が存在します.
それについては出てきたときにその都度定義します.
では、最後にまとめに入ります!!
「いろいろな行列」のまとめ
・n次正方行列とは(n,n)型行列,n×n型行列のこと
・転置行列とは,対角成分は動かさず,対面にある成分を交換させることでできる行列
入門線形代数記事一覧は「入門線形代数」

