「線形写像とは」では、写像の中でも扱いやすい線形写像という写像について扱っていこうと思います。線形写像とはベクトル空間からベクトル空間への写像で和とスカラー倍の2つの演算を保存するものです!
・線形写像とは何か理解すること
・線形写像かどうか判定できるようになること
線形写像
冒頭にも紹介しましたが線形写像とはベクトル空間からベクトル空間への写像で和とスカラー倍の2つの演算を保存するものといえます。
実際にそのことを定義しましょう。
線形写像
ベクトル空間\( V,V^{\prime} \)に対して,
\( V \)から\( V^{\prime} \)への写像\( f:V \rightarrow V^{\prime} \)が線形写像であるとは以下の二つを満たすことである.
(ⅰ)\( \mathbf{a},\mathbf{b} \in V \)に対して,\( f(\mathbf{a} + \mathbf{b}) = f(\mathbf{a}) + f(\mathbf{b}) \)
(ⅱ)\( \mathbf{a} \in V \),\( c \in \mathbb{R} \)に対して,\( f(c\mathbf{a}) = cf(\mathbf{a}) \)
このページでは簡単のためスカラーを\( \mathbb{R} \)としています.
では,線形写像の定義は上記ですが,線形写像を考えるうえで問題として問われやすいのは
写像が線形写像か否かです。
実際に例題と問を通して線形写像を判断できるようになりましょう
例題:線形写像

線形写像か確認するためには線形写像の定義にある条件(ⅰ)(ⅱ)を満たすか確認すればよいです.
また,線形写像でない場合は反例が示せば十分です.

このように,反例を示すことができれば線形写像ではないことがわかります.
この反例を見つけることはある程度の慣れが必要になるかと思いますので
いろいろな問題に当たって感覚を磨いていくといいでしょう.

それでは、もう少し次元の高いものを問としてやってみることにしましょう.
問:線形写像


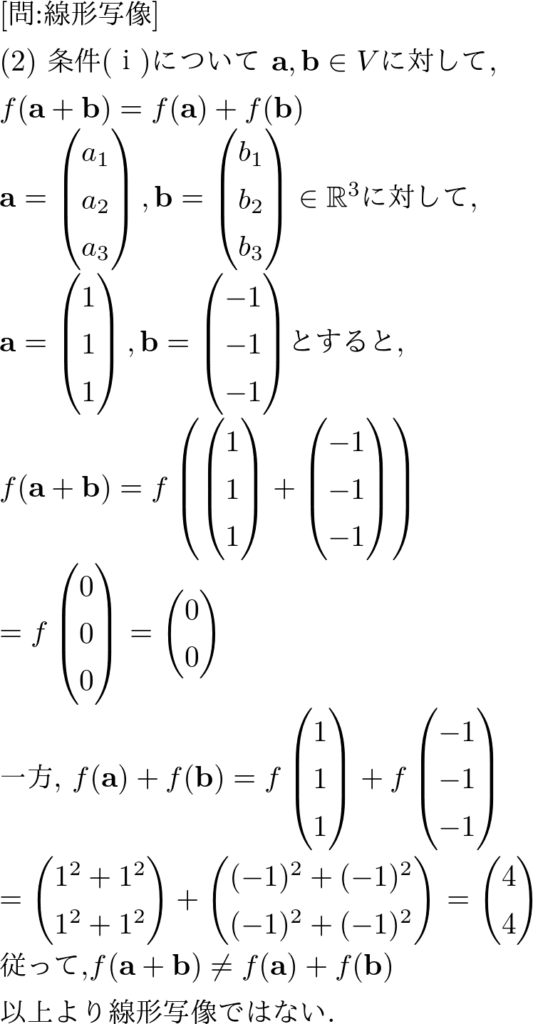
以上が「線形写像とは」という話です。
線形写像かどうか判定する問題は試験などでも頻出の重要問題ですので
しっかりおさえておきましょう!
それでは、まとめにはいります!
「線形写像とは」まとめ
\( V \)から\( V^{\prime} \)への写像\( f:V \rightarrow V^{\prime} \)が線形写像であるとは以下の二つを満たすことである.
(ⅰ)\( \mathbf{a},\mathbf{b} \in V \)に対して,\( f(\mathbf{a} + \mathbf{b}) = f(\mathbf{a}) + f(\mathbf{b}) \)
(ⅱ)\( \mathbf{a} \in V \),\( c \in \mathbb{R} \)に対して,\( f(c\mathbf{a}) = cf(\mathbf{a}) \)

