「行列の小行列式と余因子」では,n次正方行列の行列式を求める方法である行列式の余因子展開
を行う準備として行列の小行列式と余因子を計算できるようにしていきましょう!
・行列の小行列式と余因子を求めることができるようになること
目次
- 行列の小行列式と余因子
- 行列の小行列式
- 例題:行列の小行列式
- 行列の余因子
- 例題:行列の余因子
- 「n次正方行列の行列式(余因子展開)」のまとめ
行列の小行列式と余因子
まずは,余因子展開をしていく準備として行列の小行列式というものを定義します.
行列の小行列式
n次正方行列\( A = (a_{ij}) \)の第i行目と第j行目を取り除いてできる行列の行列式を
(i,j)成分の小行列式といい\( D_{ij} \)とかく.
行列の小行列式について3次正方行列の適当な成分に関する例題をつけておきますので
例題を通して一度確認することにしましょう!!
例題:行列の小行列式
3次正方行列
\( \left(\begin{array}{crl}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{array}\right) \)に対して
小行列式\( D_{11},D_{22},D_{32} \)を求めよ.
3次正方行列なので9つの成分があり
それぞれについて、小行列式が存在しますが今回は適当に(1,1)(2,2)(3,2)成分にしました.
では例題の解説に移ります
<例題の解説>
\(D_{11} = \left| \begin{array}{cc} a_{22} & a_{23}
\\ a_{32} & a_{33}\end{array}\right| \)
\(D_{22} = \left| \begin{array}{cc} a_{11} & a_{13}
\\ a_{31} & a_{33}\end{array}\right| \)
\(D_{32} = \left| \begin{array}{cc} a_{11} & a_{13}
\\ a_{21} & a_{23}\end{array}\right| \)
となります.
もちろん2次正方行列の行列式を計算してもいいですが,今回はこのままにしておきます.
さらに視覚的にみるために,この3つの例に図を加えましょう

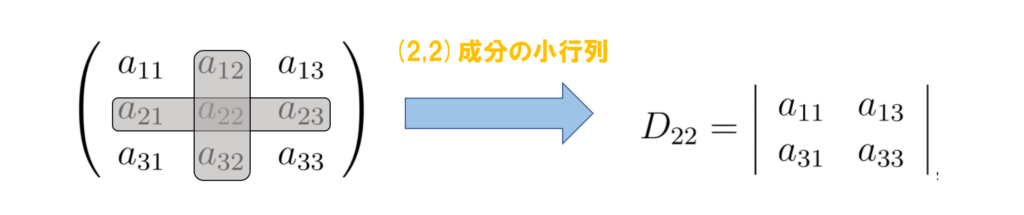
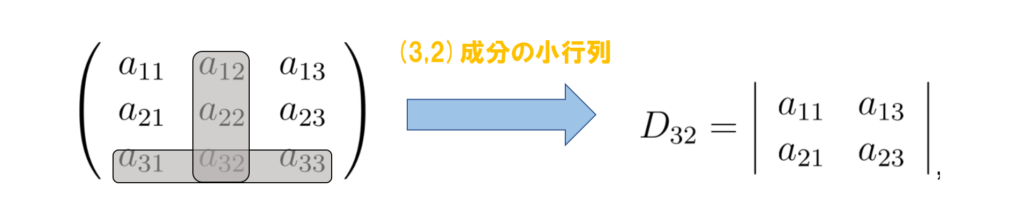
この図を見るとより鮮明に第i行目と第j行目を取り除いてできる行列の行列式
に見えてくるのではないでしょうか?
それでは,この小行列式を用いて
余因子展開に必要な行列の余因子を定義します.
行列の余因子
n次正方行列\( A = (a_{ij}) \)と\( A \)の小行列式\( D_{ij} \)に対して,
行列の(i,j)成分の小行列式に\( (-1)^{i + j} \)をかけたもの,
\( (-1)^{i + j}D_{ij} \)をAの(i, j) 成分の余因子といい\( A_{ij} \)とかく.
すなわち,\( A_{ij} = (-1)^{i + j}D_{ij} \)
余因子に関しても小行列式同様に例を用いて確認することにしましょう
例題:行列の余因子
3次正方行列
\( \left(\begin{array}{crl}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{array}\right) \)に対して
余因子\( A_{11},A_{22},A_{32} \)を求めよ.
<例題の解答>
\(A_{11} = (-1)^{1 + 1}D_{11} = \left| \begin{array}{cc} a_{22} & a_{23}
\\ a_{32} & a_{33}\end{array}\right| \)
\(A_{22} = (-1)^{2 + 2}D_{22} = \left| \begin{array}{cc} a_{11} & a_{13}
\\ a_{31} & a_{33}\end{array}\right| \)
\(A_{32} = (-1)^{3 +2}D_{32} = (-1)\left| \begin{array}{cc} a_{11} & a_{13}
\\ a_{21} & a_{23}\end{array}\right| \)
ここまでが余因子展開を行うための準備です.
しっかりここまでの操作を復習して余因子展開を勉強するようにしましょう.
この小行列式と余因子を用いてn次正方行列の行列式を求める余因子展開という方法は
こちらの記事で紹介しています!
では,まとめに入ります!
「行列の小行列式と余因子」のまとめ
・行列の小行列式とは,第i行目と第j行目を取り除いてできる行列の行列式
・行列の余因子とは(i,j)成分の小行列式に\( (-1)^{i + j} \)をかけたもの
入門線形代数記事一覧は「入門線形代数」

