「和空間と共通部分」では,ベクトル空間の部分空間の中でも特別に名前のついている
和空間と共通部分について扱っていきます.
和空間や共通部分は後に次元を求める際に頻出の問題になりますのでここでどんなものかおさえておきましょう!
・部分空間の和空間と共通部分を理解すること
部分空間の和空間と共通部分
部分空間の和空間と共通部分
早速どんな部分空間になるのか見ていきましょう!
\( W_1,W_2 \)がベクトル空間\( V \)の部分空間であるとき
・\( W_1 + W_2 = \left\{ \mathbf{w_1} + \mathbf{w_2} \mid \mathbf{w_1} \in W_1,\mathbf{w_2} \in W_2\right\} \)
・\( W_1 \cap W_2 = \left\{ \mathbf{w_1} \cap \mathbf{w_2} \mid \mathbf{w_1} \in W_1,\mathbf{w_2} \in W_2\right\} \)
は、\( V \)の部分空間であり,
\( W_1 + W_2 \)のことを和空間
\( W_1 \cap W_2 \)のことを共通部分という
部分空間であるかどうかは部分空間であることを示すいい問題になります.
今回は和空間を問としてつけておきますので,是非自力で確認してみてください.
もし,部分空間であることの示し方を忘れてしまっている方は「部分空間」を復習してから取り組むとよいでしょう!
\( W_1,W_2 \)がベクトル空間\( V \)の部分空間であるとき
和空間\( W_1 + W_2 = \left\{ \mathbf{w_1} + \mathbf{w_2} \mid \mathbf{w_1} \in W_1,\mathbf{w_2} \in W_2\right\} \)
は、\( V \)の部分空間であることを示せ.
部分空間かどうか確認するためには、部分空間で定義した(S-0)~(S-2)の内容を確認すればいいですので\( W_1 + W_2,W_1 \cap W_2 \)のそれぞれに対して(S-0)~(S-2)を確認していきましょう.
まずは,和空間についてです.

共通部分については以下の問として確認していくことにしましょう.
\(\mathbb{R}^2\)の部分空間
\( W_1 = \left\{ \left. \begin{pmatrix} x\\y \end{pmatrix} \in \mathbb{R}^2 \right| x – y = 0 \right\} \)
\( W_2 = \left\{ \left. \begin{pmatrix} x\\y \end{pmatrix} \in \mathbb{R}^2 \right| 2x + y = 0 \right\} \)
について,\( W_1 \cap W_2 \)は\( \mathbb{R}^2 \)の部分空間であることを示せ.
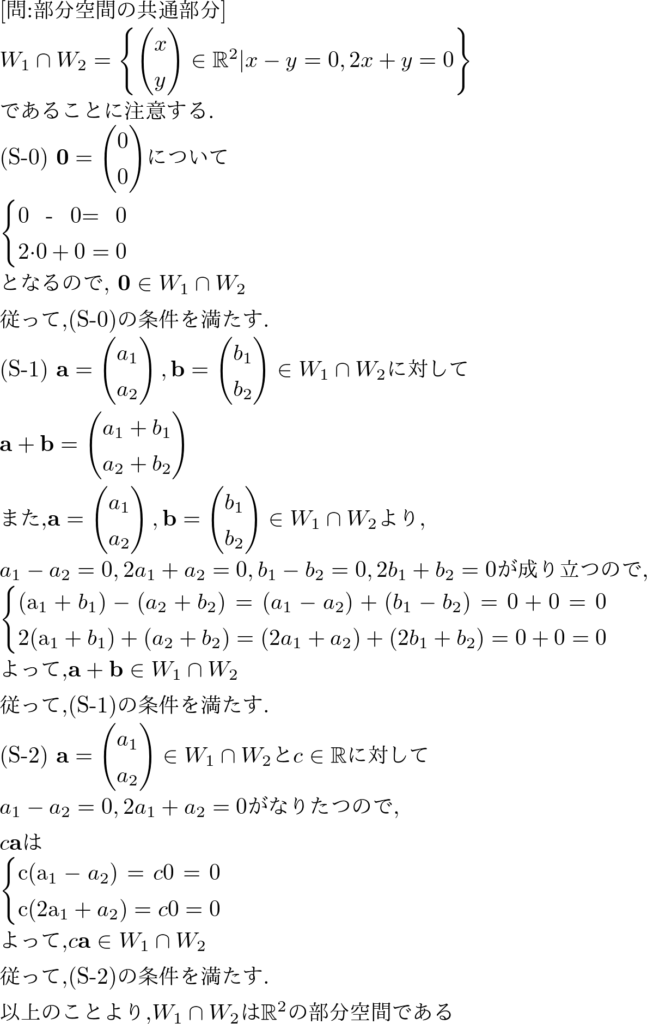
以上が「和空間と共通部分」という話です.
冒頭にも言いましたが,和空間と共通部分の次元を求める問題は試験に頻出ですので,
この記事で行った部分空間の判定がしっかりできておくようになると
その場面でも有効になりますので、しっかりとマスターしておきましょう!
それではまとめに入ります!
「和空間と共通部分」まとめ
部分空間の
・和空間は\( W_1 + W_2 \)のこと
・共通部分は\( W_1 \cap W_2 \)のこと
入門線形代数記事一覧は「入門線形代数」

