【入門線形代数】写像とは？(全射・単射)-線形写像-

「写像とは？」では写像という線形代数に限らずほかの単元でもとても大切になってくる概念を勉強していこうと思います。
写像とは何かということと全射・単射・全単射という写像の種類を見分けることができることになることを目標に勉強していきましょう!!

写像とは？

では早速,写像の定義をみていきます.

写像とは？

写像に関しての定義を見てパッと理解できる人は少ないかと思います。
今回は写像に関して図をベースに理解していくことにしましょう

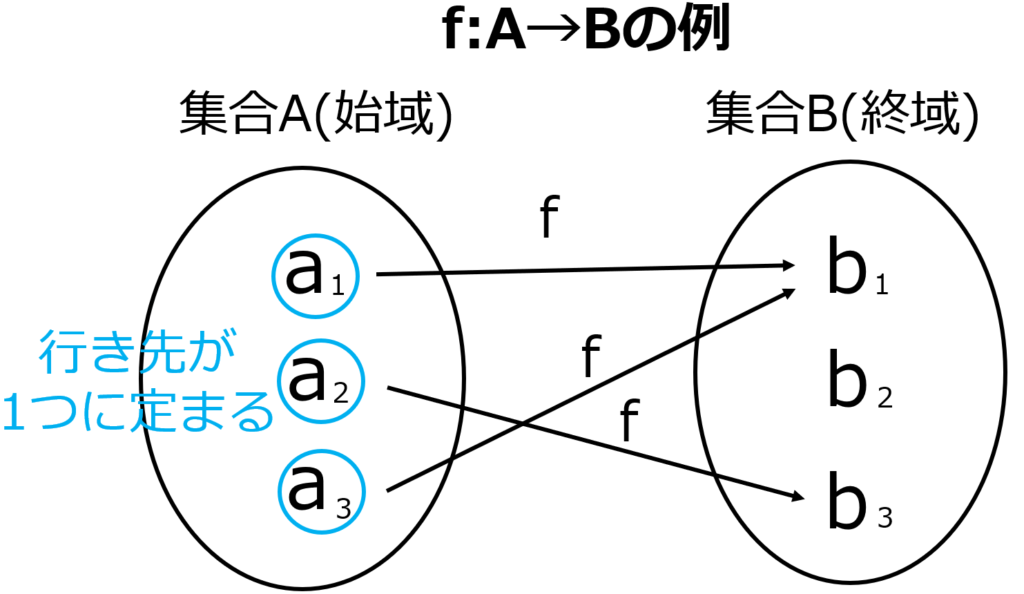
写像とは図のように\( A \)のどの元に対しても１つの行き先が１つだけ定まる
ような規則を言います.

この図を見て\( a_1a_3 \)の行き先が\( b_1 \)に被っているけどだいじょうぶなの？と思われた方がいるかもしれません。
結論、問題ありません。

なぜなら、\( a_1a_3 \)どちらも\( b_1 \)という1つの行き先に定まっています。
従って対応先が1つに定まりますので写像の定義から問題ありません.

では逆に、上に対して写像とはならない例を見ていきましょう。

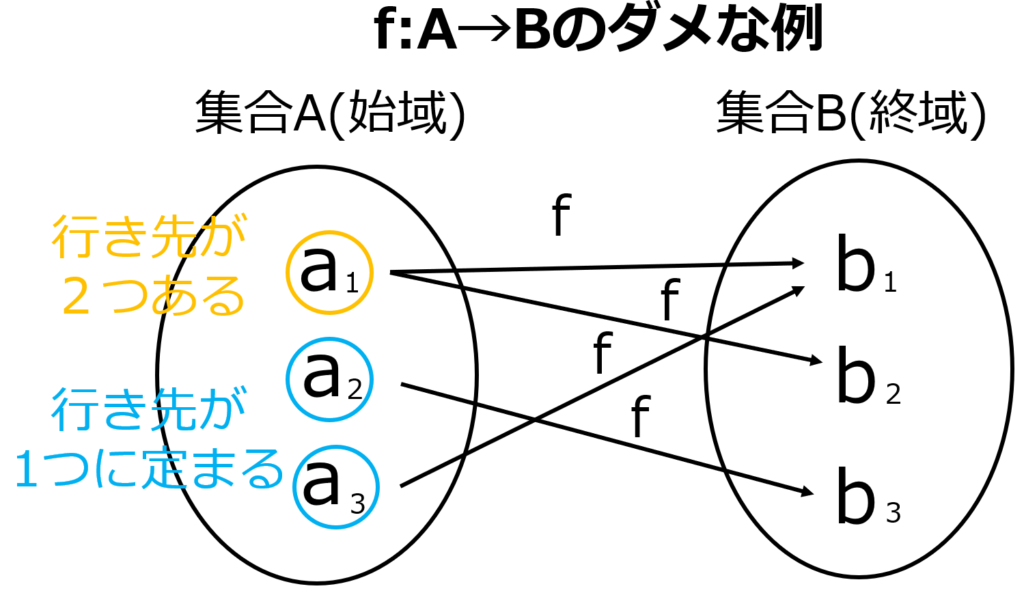
上図のパターンは\( a_1 \)の行き先が\( b_1 \)と\( b_2 \)の二つあり行き先が２つあり1つに定まっていませんね.

このような規則は写像と呼びません.
あくまで写像というときは写した先が1つに定まります.

ここまで写像の定義です。
ここからは写像を全射・単射・全単射という種類に分けていきましょう。

全射・単射・全単射

全射・単射・全単射

全射・単射・全単射についてもそれぞれの例を通して理解を深めていきましょう.

全射性

全射の例をみてみましょう

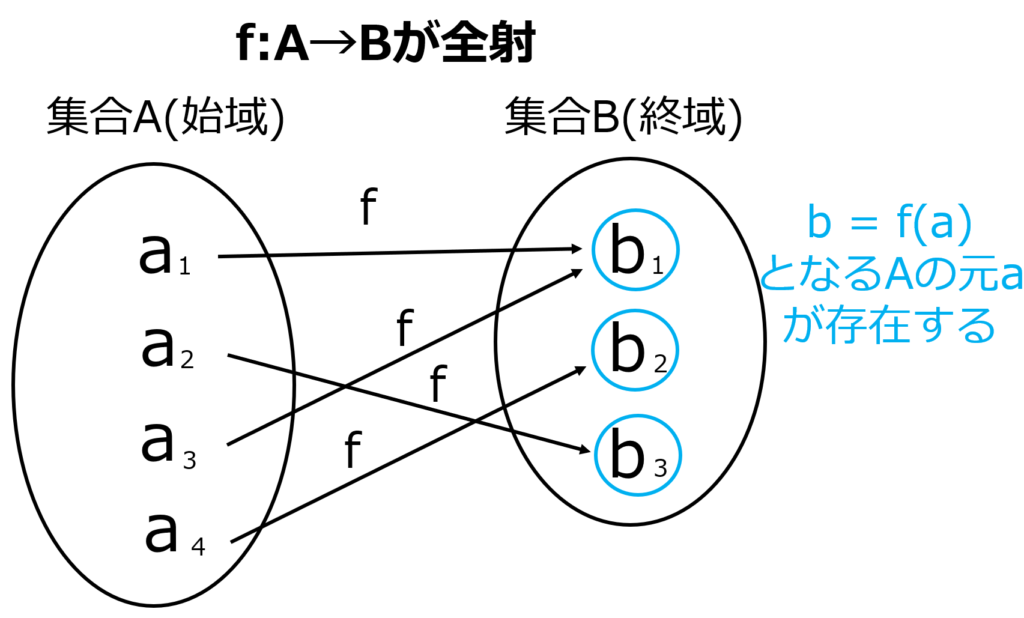
\( b_1 \)に対しては\( b_1 = f(a_1),f(a_3) \)となり\( A \)の元\( a_1,a_3 \)が存在.
\( b_2 \)に対しては\( b_2 = f(a_4) \)となり\( A \)の元\( a_4 \)が存在.
\( b_3 \)に対しては\( b_3 = f(a_2) \)となり\( A \)の元\( a_2 \)が存在.

これは全射の定義「\( B \)の任意の元bに対しても\( b = f(a) \)となる\( A \)の元\( a \)が常に存在する.」を満たしています.

一方、全射とはならない例を見ていきましょう

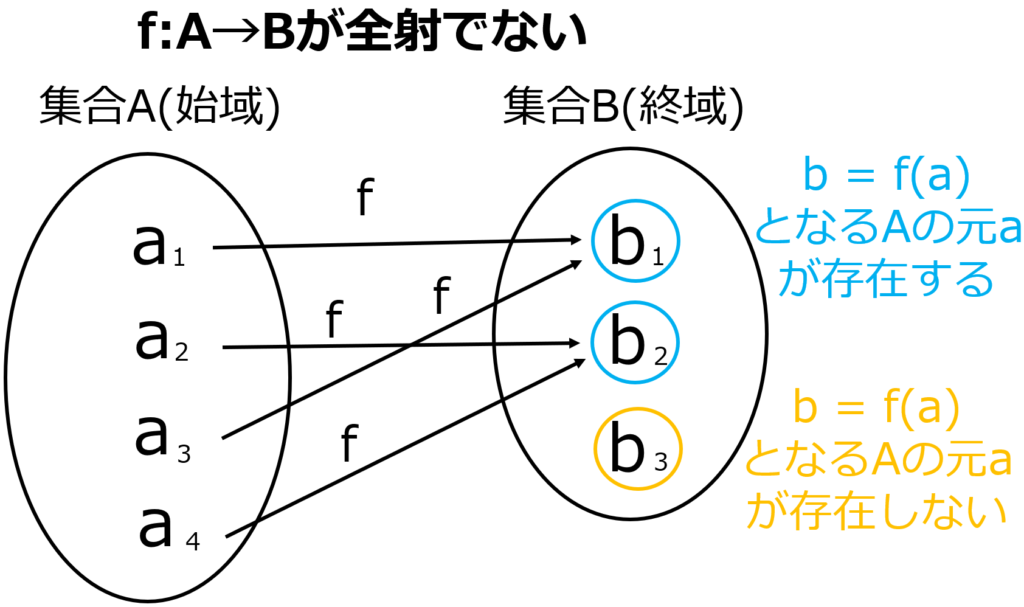
これは\( b_1 \)に対しては\( b_1 = f(a_1),f(a_3) \)となり\( A \)の元\( a_1,a_3 \)が存在.
\( b_2 \)に対しては\( b_2 = f(a_2),f(a_4) \)となり\( A \)の元\( a_2,a_4 \)が存在.

ですが,

\( b_3 \)に対しては\( b = f(a) \)となる\( A \)の元が存在しません.
なのでこの場合は全射とは言えません.

単射性

単射の例をみてみましょう

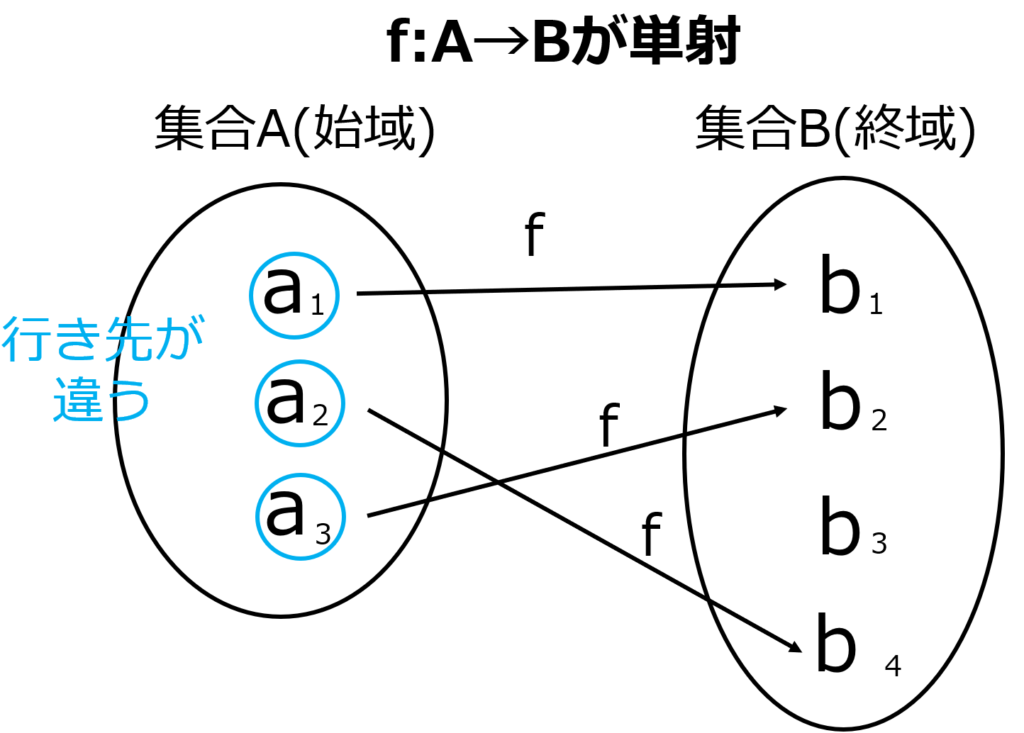
\( A \)の各元\( a_1,a_2,a_3 \)に対して

それぞれ\( f(a_1),f(a_2),f(a_3) \)は\( f(a_1) = b_1,f(a_2) = b_4,f(a_3) = b_2 \)となり違う行き先に向かっています.

一方、下のような場合は全射ではありません

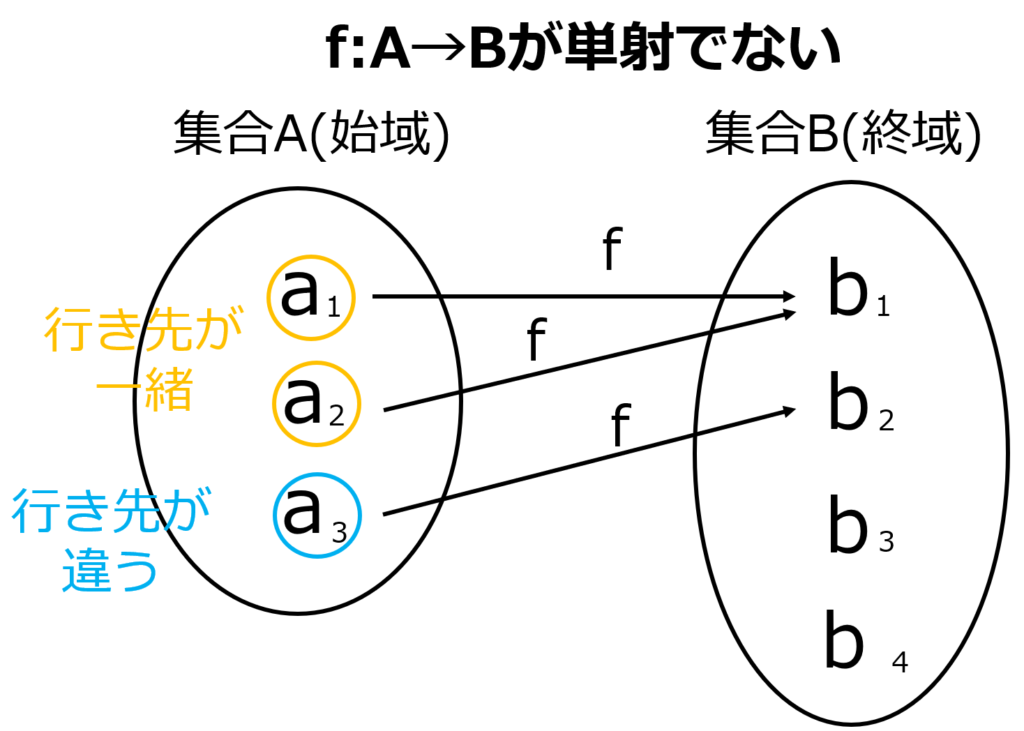
\( A \)の各元\( a_1,a_2,a_3 \)に対して
それぞれ\( f(a_1),f(a_2),f(a_3) \)は\( f(a_1) = f(a_2) = b_1,f(a_3) = b_2 \)となり\( a_1,a_2 \)の行き先が同じ\( b_1 \)になっています.

このような場合単射とは言いません.

全単射

全単射も例をみましょう。

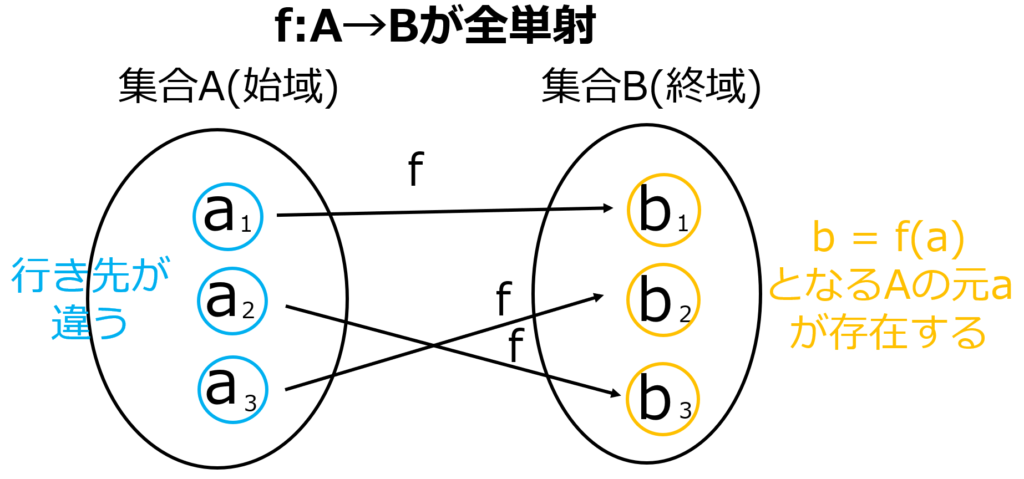
ここまでみてきた全射と単射であることの条件を同時に満たしています
なのでこの例は全単射といえるわけですね.

全単射ではない例に関しては
実は,「fが全射」の例の2つと「fが単射」の例の２つがいずれも
全単射ではない例です.
すなわち,全射か単射またはその両方を満たしていません.
なのでこれは練習として何が全単射といえない理由なのか確認してみるとよいでしょう.

以上が「写像とは?」という話です.
写像の話は線形代数だけではなく,微分積分やその他さまざまな分野で登場しますのでしっかり押さえてしまいましょう！

それでは、まとめに入ります！

「写像とは?」まとめ