ベクトルは向きと大きさはベクトルの長さと向いている方法に依存していましたが,
もっと明確に表現する方法としてベクトルの成分表示を学んでいきましょう.
この成分表示を使えば上で感覚的なベクトルの大きさや向きについてが
実際に数値として計算可能になります!
・基本ベクトルと位置ベクトルとは何か理解すること
・ベクトルの成分表示について理解すること
・成分表示されたベクトル同士を演算できるようになること
ベクトルの成分
早速ベクトルの成分表示の第1段階として基本ベクトルと位置ベクトル
というベクトルを定義します!
基本ベクトルと位置ベクトル
空間上にOを原点とする直交座標系を設定する.
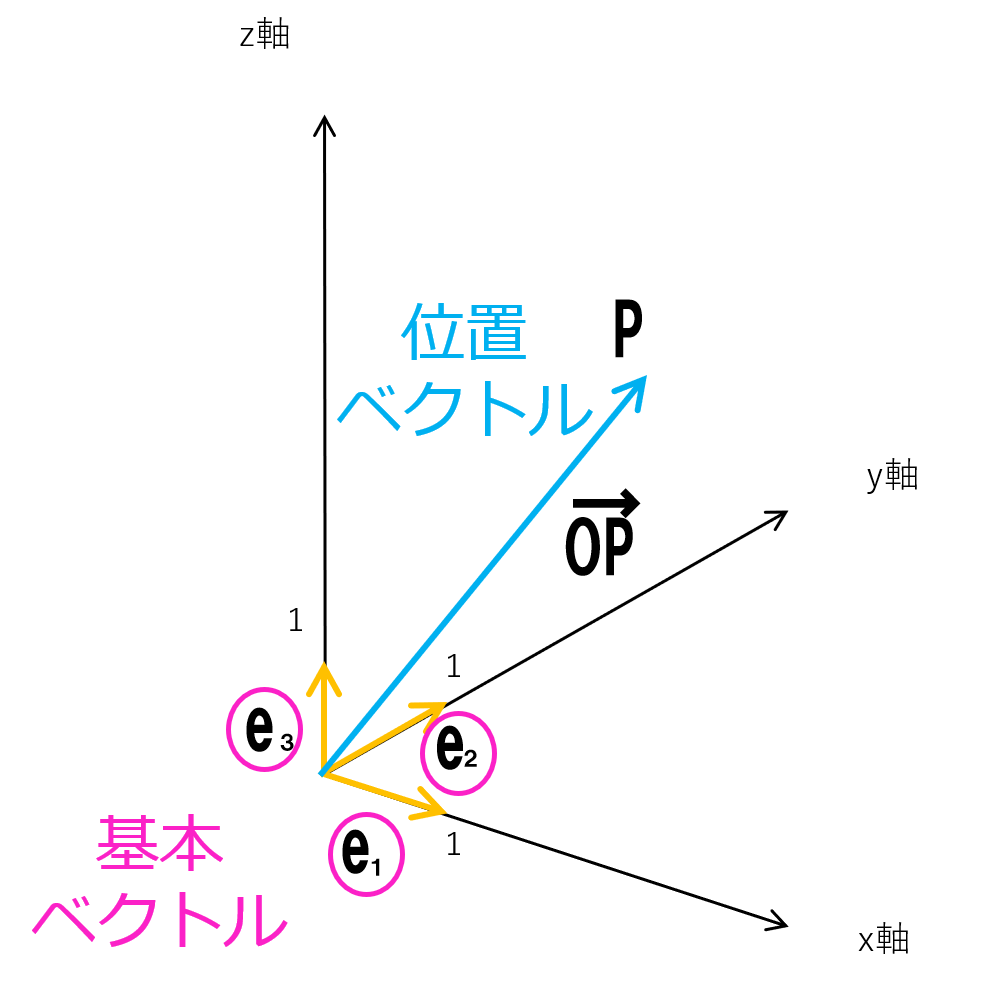
Oを始点としてx軸,y軸,z軸上に正の向きを持つ単位ベクトルをそれぞれ
\( \mathbf{e_{1},e_{2},e_{3}}\)と書き,基本ベクトルという.
また、Oを始点とするベクトル\( \mathbf{x} = \vec{OP}\)を点Pの位置ベクトルという.
この定義で出てきている単位ベクトルとは大きさが1のベクトルのことです.
この基本ベクトルに関しては図を用いて説明していくことにしましょう!
今回は空間として3次元の空間を考えましたが,
人間には想像できませんが,
4次元の場合でも基本ベクトル\( \mathbf{e_{1},e_{2},e_{3},e_{4}}\)を用いれば
表現は可能です.
あくまで考えやすいから3次元を例にとっただけです.
では,このことを用いて成分表示を考えていきましょう!
ベクトルの成分表示
点Pの座標を\( (x_1,x_{2},x_{3})\)とすれば,点Pの位置ベクトル\( \mathbf{x}\)は基本ベクトルを用いて
\( \mathbf{x} = x_1\pmb{e_{1}} + x_{2}\pmb{e_{2}} + x_{3}\pmb{e_{3}}\)
と表される.
このときの\( x_1,x_{2},x_{3}\)をベクトル\( \mathbf{x}\)のx成分,y成分,z成分といい\( \mathbf{x} = \begin{pmatrix} x_{1}
\\ x_{2}
\\ x_{3} \end{pmatrix}\)
を\( \mathbf{x}\)の成分表示という.
定義をすこし考察していこうと思います.
成分表示は基本ベクトルをそれぞれの成分に関してスカラー倍して足したものです!
このことを視覚化して上の図にさらに成分表示の要素を加えたものが以下です.
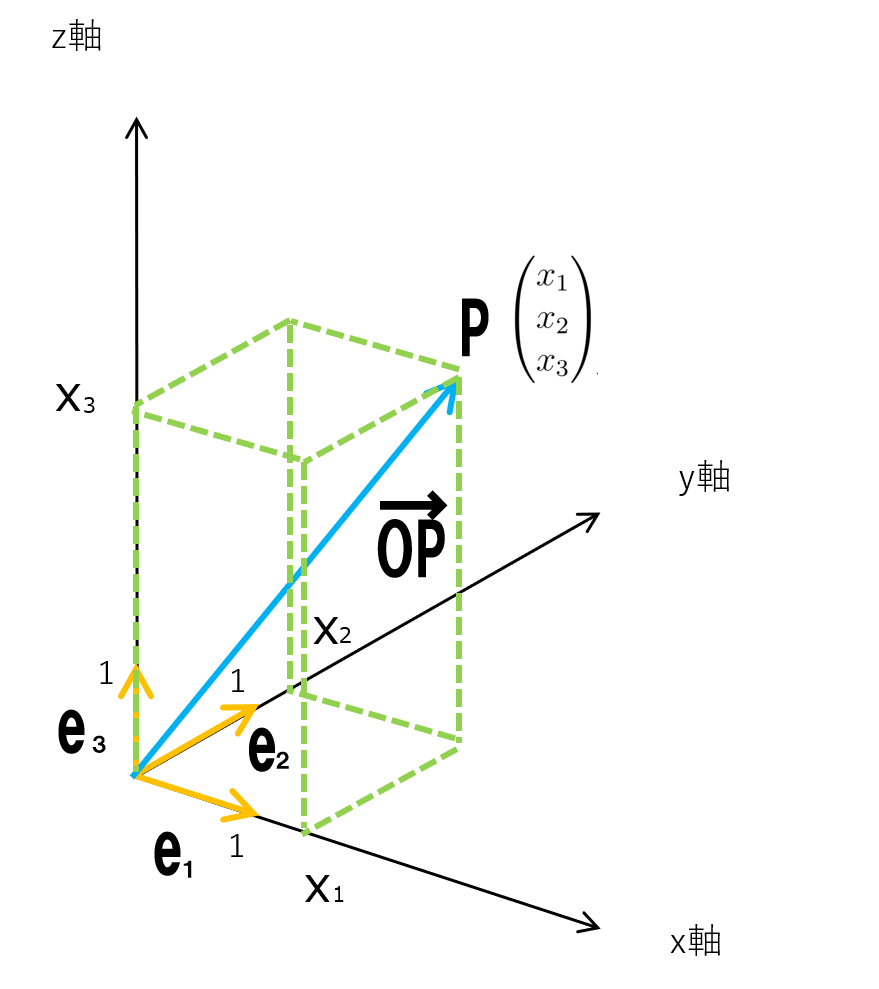
今回の図では,\( \vec{OP} = x_1\pmb{e_{1}} + x_{2}\pmb{e_{2}} + x_{3}\pmb{e_{3}}\)
となっています.
この長方形の各辺で\( x_1\pmb{e_{1}}, x_{2}\pmb{e_{2}}, x_{3}\pmb{e_{3}}\)を表しています.
この直方体の大きさを変えることでベクトル全体が表現できます.
では,成分表示されたベクトルに対して成り立つ演算についてみていくことにしましょう!
定理:ベクトルの成分表示

簡単な説明を加えます.
(1)すべての成分が等しければ同じベクトルであることを保証しています.
これは,当たり前といえば当たり前のことですね笑
(2)和とスカラー倍についても「ベクトルの和とスカラー倍」で定義した
ものが成分に対して成り立つことを保証しています
(3)ベクトルの大きさについては中学生の時に習った三平方の定理を少し拡張したものですね
では,この定理を用いて実際に問題を解いていくことにしましょう!
例題:ベクトルの成分表示
ベクトル\( \mathbf{a} = \begin{pmatrix} 3
\\4 \end{pmatrix},\mathbf{a} = \begin{pmatrix} 3
\\-2 \end{pmatrix}\)に対して,以下の問に答えよ
(1)\( \mathbf{a} + \mathbf{b}\)
(2)\( 2\mathbf{a}- 3\mathbf{b}\)
(3)\( \|\mathbf{a}\|,\|\mathbf{b}\|\)
(4)\( \| 2\mathbf{a} – 3\mathbf{b} \|\)
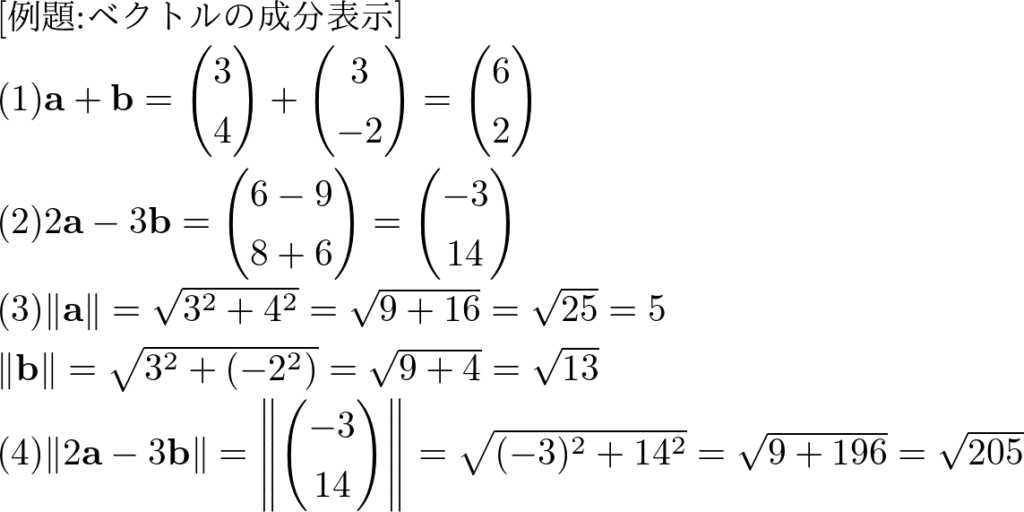
問:ベクトルの成分表示
ベクトル\( \mathbf{a} = \begin{pmatrix} 4
\\3
\\0 \end{pmatrix},\mathbf{b} = \begin{pmatrix} -1
\\2
\\-2 \end{pmatrix},\mathbf{c} = \begin{pmatrix} 2
\\4
\\7 \end{pmatrix}\)に対して,以下の問に答えよ.
(1)\( \mathbf{a} + \mathbf{b},\mathbf{a} + \mathbf{c},\mathbf{b} + \mathbf{c}\)
(2)\( 2\mathbf{a},3\mathbf{b},-2\mathbf{c}\)
(3)\( \| \mathbf{a} \|,\| \mathbf{b} \|,\|\mathbf{c} \|\)
(4)\( \| \mathbf{b} + \mathbf{c} \|\)

以上が「ベクトルの成分」という話です!
この成分を勉強すると向きと大きさで定義されたベクトルが
具体的な数値となり見やすくなります.
それではまとめに入ります!
「ベクトルの成分」まとめ
・基本ベクトルとは,原点を始点とする直交座標軸上の正の向きの単位ベクトル
・点Pの位置ベクトルとは,Oを始点とするベクトル\( \mathbf{x} = \vec{OP}\)
・ベクトルの成分表示とは点Pの位置ベクトル\( \mathbf{x}\)は基本ベクトルを用いて
\( \mathbf{x} = x_1\pmb{e_{1}} + x_{2}\pmb{e_{2}} + x_{3}\pmb{e_{3}}\)
と表したときの\( \begin{pmatrix} x_{1}
\\ x_{2}
\\ x_{3} \end{pmatrix}\)

