「一次結合と生成系」ではのちに一次従属と一次独立で勉強する際に重要になる一次結合と
生成系というベクトル空間の基盤となるものを扱っていこうと思います.
どちらも知っておかないとこの先の学習がしづらくなってしまいますので是非しっかりと
おさえてしまいましょう!
・一次結合とはなにか理解すること
・生成系と張られる空間とはなにか理解すること
一次結合と生成系
一次結合
ベクトル空間\(V \)のn個のベクトル\(\mathbf{a_1,a_2, \cdots ,a_n} \)と
n個のスカラー\(c_1,c_2 \cdots c_n \in \mathbb{R} \)に対して
\( c_1\mathbf{a_1}+c_2\mathbf{a_2}+ \cdots +c_n\mathbf{a_n} \)
を\({\mathbf{a_1,a_2 \cdots a_n}} \)の一次結合といい,
一次結合全体の集合を\( <\mathbf{a_1,a_2, \cdots ,a_n}> \)と表す.
一次結合は別名として線形結合ということもあります.
一次結合について簡単にまとめると
一次結合とは,”スカラー倍した各ベクトルの和”のことです.
この一次結合全体の集合は\(V\)の部分空間になりますので,
このことに名前を付けたものが以下の生成系というものです.
張られる空間と生成系
ベクトル空間Vのn個のベクトル\(\mathbf{a_1,a_2, \cdots ,a_n} \)と
n個のスカラー\(c_1,c_2 \cdots c_n \in \mathbb{R} \)に対して
一次結合全体の集合\( <\mathbf{a_1,a_2, \cdots ,a_n}> \)はVの部分空間であることから,
Vは\(\mathbf{a_1,a_2, \cdots ,a_n}\)から生成される部分空間である.
または,
Vは\(\mathbf{a_1,a_2, \cdots ,a_n}\)によって張られる部分空間である.
といい,\( \left\{ \mathbf{a_1,a_2, \cdots ,a_n} \right\} \)をその部分空間の生成系という
生成される部分空間も張られる部分空間も意味は一緒でどちらも
使われる言葉なので意味をしっかり理解しておきましょう.
特に張られる空間という言葉は少し独特ですので,しっかり覚えておくとよいでしょう.
張られる空間という言葉はベクトル空間の学習が進むと馴染んでくると思います.
では,この一次結合と生成系の簡単な例を一つ見てみることにしましょう
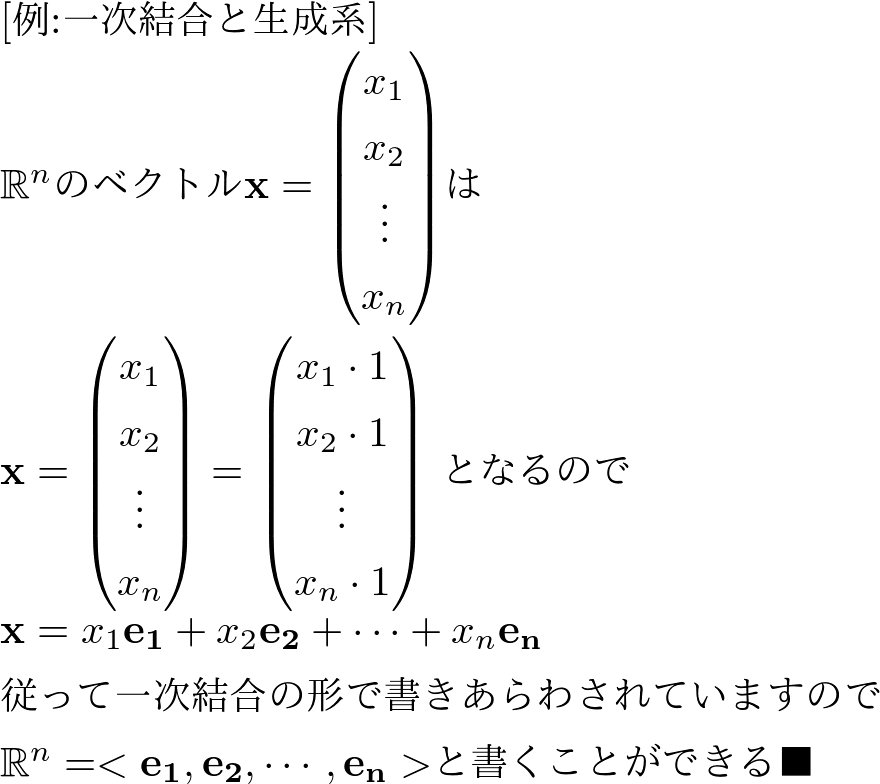
例:一次結合と生成系
\( \mathbb{R}^n \)とそのベクトル\( \mathbf{e_1}= \begin{pmatrix} 1
\\0
\\ \vdots
\\0
\end{pmatrix},\mathbf{e_2}= \begin{pmatrix} 0
\\1
\\ \vdots
\\0
\end{pmatrix},\cdots,\mathbf{e_n}= \begin{pmatrix} 0
\\0
\\ \vdots
\\ 1
\end{pmatrix} \)を用いて
\( \mathbb{R}^n = <\mathbf{e_1},\mathbf{e_2},\cdots,\mathbf{e_n}> \)とかける.
この例では,
基本ベクトルは\( \mathbb{R}^{n} \)の生成系である.
言い換えると\( \mathbb{R}^{n} \)は基本ベクトルにより張られる空間である.
ということを言っています.
実際に\( \mathbb{R}^n = <\mathbf{e_1},\mathbf{e_2},\cdots,\mathbf{e_n}> \)
を確認してみましょう.
以上が「一次結合と生成系」という話です.
冒頭にも話しましたが,今後この先一次結合や一次従属というベクトル空間の大テーマを
扱うに対して重要な単元ですので,
しっかりと理解しておきましょう!
それではまとめに入ります!
「一次結合と生成系」まとめ
・一次結合とは,”スカラー倍した各ベクトルの和”
・生成系とは,一次結合全体の集合を構成するベクトル
入門線形代数記事一覧は「入門線形代数」

