「1次,2次,3次正方行列の行列式」では低い次元での行列式を定義していこうと思います!
一般のn次元の正方行列とは異なり3次までは特別に計算法がありますので,それをしっかり学んでいくことにしましょう!
・1,2,3次正方行列の行列式を計算できるようになること
行列の行列式
冒頭でも行列式という言葉が出てきていますが,そもそも行列式ってなんだという話だと思うので,早速定義をしましょう.
行列の行列式
n次正方行列Aをある規則に従って計算した結果を行列の行列式といい、
\( | A | , \mathrm{det}A \)とかく.
ある規則ってなんだよ!
と思われた方もいるかもしれませんが,それは学習していくなかでひとつづつ学んでいくことにするとしましょう笑
ちなみに,\( \mathrm{det}A \)の\( \mathrm{det} \)とは
行列式を表す英単語determinantの頭文字です.
では,一番単純な行列式として1次,2次正方行列の行列式を定義します!
1次,2次正方行列の行列式
1次正方行列\( \begin{pmatrix}a\end{pmatrix} \)の行列式は
\( |a| = a \)
2次正方行列\( \left(\begin{array}{cc}a_{11} & a_{12}\\a_{21} &a_{22}\end{array}\right) \)の行列式は
\( \left| \begin{array}{cc}a_{11} & a_{12}\\a_{21} &a_{22}\end{array} \right| = a_{11}a_{22} – a_{12}a_{21} \)となる.
1次正方行列に関しては、意外と触れられていないことがあるのですが
成分がそのまま行列式の値となります.
2次正方行列に関しては、成分を斜めに掛け算して引き算します.
実際のイメージをつかむために図を加えます.
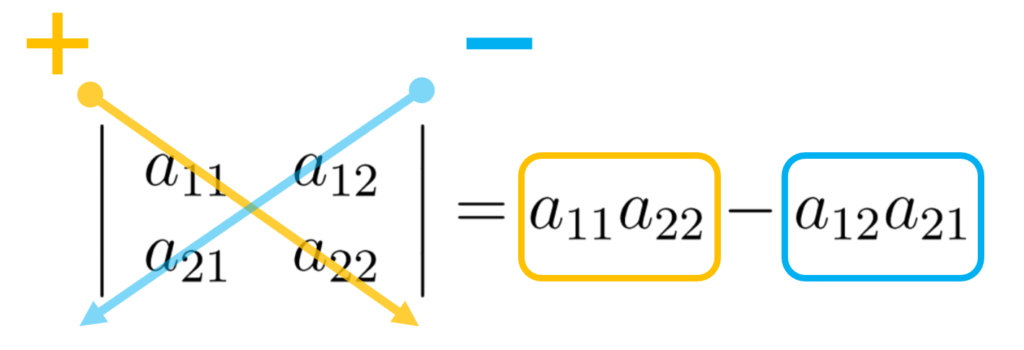
これは、3次正方行列の時にも使いますのでしっかり覚えておきましょう.
覚え方の一つとして、図のように色もセットで覚えるといいかと思います.
オレンジがプラスイメージ、ブルーがマイナスイメージと覚えると忘れにくいと思います.
最初の内はプラスとマイナスがよくわからなくなるので意識して覚えておくとよいでしょう.
では,ここまでの計算を例題を用いて確認していくことにしましょう.
例題:1次,2次正方行列の行列式
以下の行列式を求めよ.
\( (1)\begin{pmatrix}5\end{pmatrix} \)
\( (2)\left(\begin{array}{cc}1 & 0\\0 &1\end{array}\right) \)
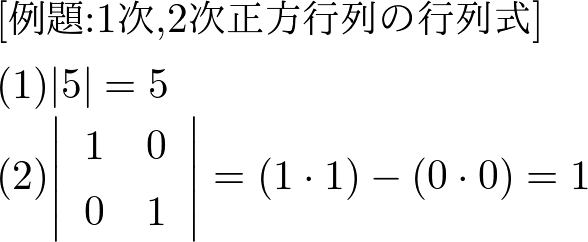
では,この例題を参考にして問を解いてみることにしましょう.
問:1次,2次正方行列の行列式
以下の行列式を求めよ.
\( (1)\begin{pmatrix}-2\end{pmatrix} \)
\( (2)\left(\begin{array}{cc}2 & -1\\3 &1\end{array}\right) \)

(1)のように負の一次正方行列だと絶対値のように見えてしまいますが
あくまでも行列式を求める問題ですので,成分がそのまま出てきます.
もし見にくければdetを使って\( \mathrm{det}(-2) = -2 \)と書いても良いと思います.
では次に3次正方行列の行列式を求めていきましょう!
サラスの公式(3次正方行列の行列式)
3次正方行列の行列式は特別にサラスの公式という名前がついていますので
この名前で定義します.
サラスの公式
3次正方行列\( \left(\begin{array}{crl}a_{11} & a_{12} & a_{13}
\\a_{21} & a_{22} & a_{23}
\\a_{31} & a_{32} & a_{33}\end{array}\right) \)の行列式は以下である.
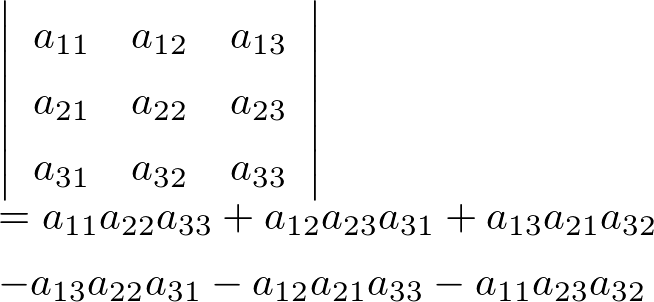
2次正方行列の時に3次正方行列の行列式でも使うので図をよく覚えておくと良いでしょう
と告知したように斜め掛けがここでも大切です.
では、図を用いて確認していきましょう.
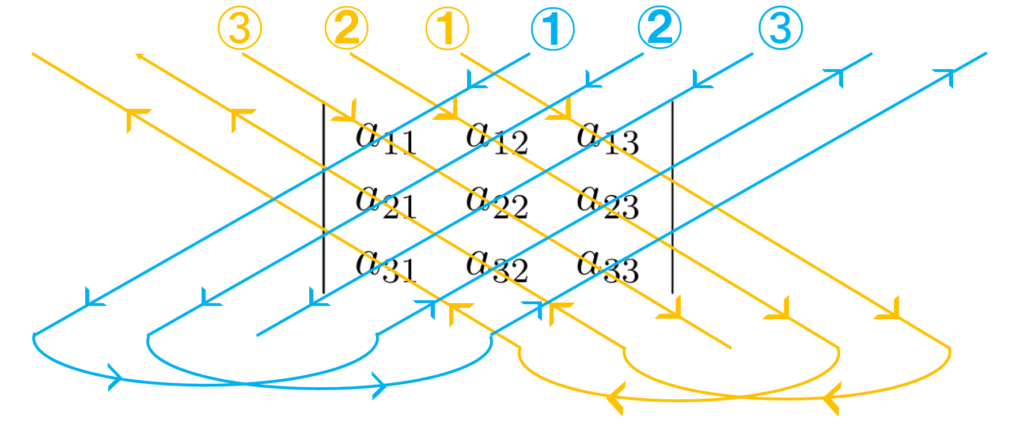
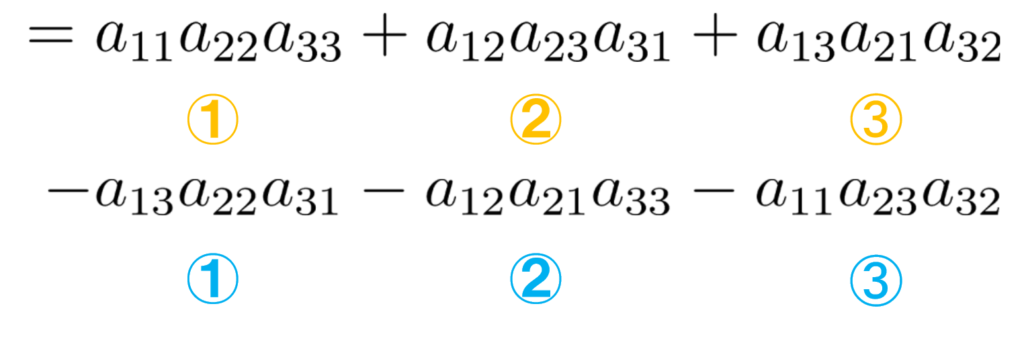
上図の通り2次正方行列の行列式と同じ向きで+とーがつきます.
細かく言葉で説明するより図で理解したほうがわかりやすいかと思いますので
図を参考にしてください.
サラスの公式の絶対におさえて欲しい注意点を挙げます.
サラスの公式は3次正方行列にしか使えません.
4次正方行列などに適応しようとすると計算が合わなくなるので
必ず、3次正方行列のみに使うようにして下さい.
それでは、3次正方行列に関しても実際に例題を解いて行列式を確認していきましょう.
例題:サラスの公式
次の行列の行列式を求めよ.
\( \left(\begin{array}{crl}2 & 1 & 1
\\-1 & 1 & 3
\\-2 & 0 & 1\end{array}\right) \)
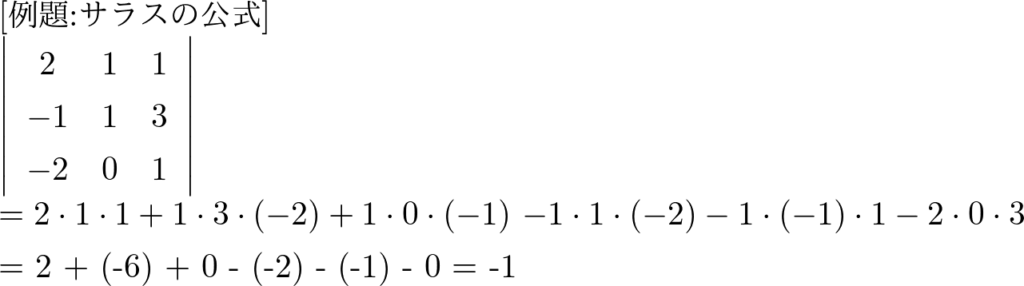
問:サラスの公式
次の行列の行列式を求めよ.
\( \left(\begin{array}{crl}4 & 3 & 1
\\-1 & 2 & 3
\\-1 & 1 & 2\end{array}\right) \)
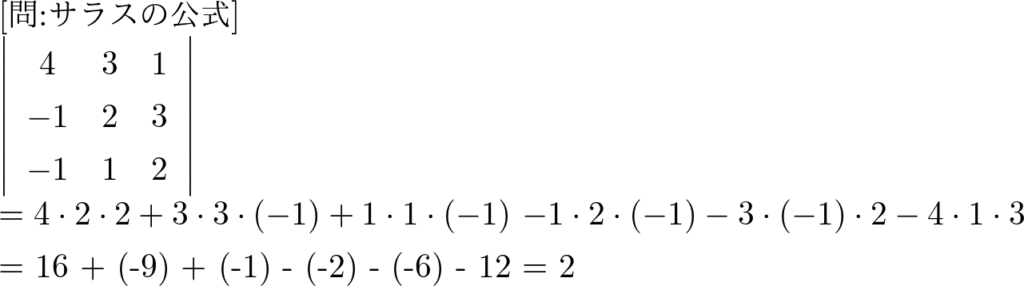
以上が「1次,2次,3次正方行列の行列式」の話です.
2次や3次はよく符号の間違いがありますので,注意してください!!
この行列式の話は以降の単元でも必須になってきますので必ずおさえておきましょう!
それではまとめに入ります!
「1次,2次,3次正方行列の行列式」のまとめ
・1次正方行列の行列式は,成分がそのまま行列式.
・2次正方行列の行列式は,成分を斜めに掛け算して引き算.
・3次正方行列の行列式は,サラスの公式.
入門線形代数記事一覧は「入門線形代数」

