「ベクトルの和とスカラー倍」では,ベクトルの演算として
和とスカラー倍を考えていこうと思います.
この和とスカラー倍を勉強することでベクトルを足したり伸縮を考えることができるように
なりますので,ぜひしっかりとマスターしましょう
・ベクトルの和とスカラー倍についてどのようになるのか理解する.
ベクトルの演算
まずは演算を考える前にそもそものベクトルを足すことと
スカラー倍することを定義します!
ベクトルの和とスカラー倍
(ベクトルの和)
二つのベクトル\( \mathbf{a} = \vec{AB},\mathbf{b} = \vec{BC}\)に対して
\( \mathbf{c} = \vec{AC}\)とおく,このとき
\( \mathbf{c} = \mathbf{a} + \mathbf{b}\)を
\( \mathbf{a}, \mathbf{b}\)の和という.
(ベクトルのスカラー倍)
ベクトル\( \mathbf{a}\)と\( k \in \mathbb{R}\)に対して
スカラー倍\( k\mathbf{a}\)を以下のように定める.
(ⅰ)k>0のとき,向きは\( \mathbf{a}\)と同じ、大きさは\( \mathbf{a}\)のk倍.
(ⅱ)k<0のとき,向きは\( \mathbf{a}\)と反対、大きさは\( \mathbf{a}\)のk倍
(ⅲ)k=0のとき,零ベクトル\( 0\).
スカラー倍に関しては今回は実数で考えていますが,複素数を考えても問題ありません.
この和とスカラー倍について図を用いてイメージを膨らませていきましょう!
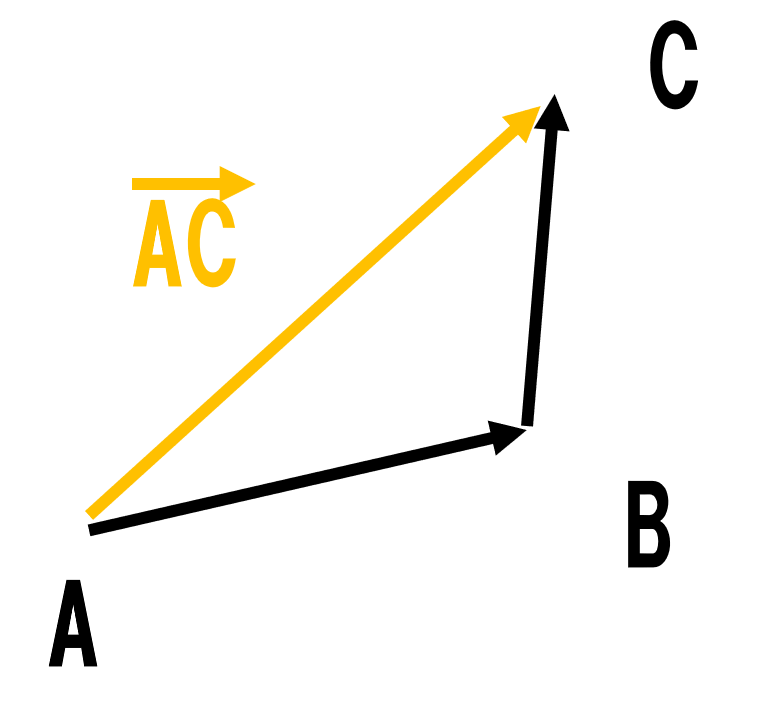
まずはベクトルの和についてです!
\( \mathbf{a} + \mathbf{b}\)は\( \vec{AB} + \vec{BC}\)のことですから,
日本語で書きあらわすと
(AからCにむかうベクトル) = (AからBに向かうベクトル) + (BからCに向かうベクトル)
これを図にすると下のようになります.
では次にスカラー倍をみていきます.
(ⅰ)k>0のときは同じ方向にk倍させるので下のようになります.
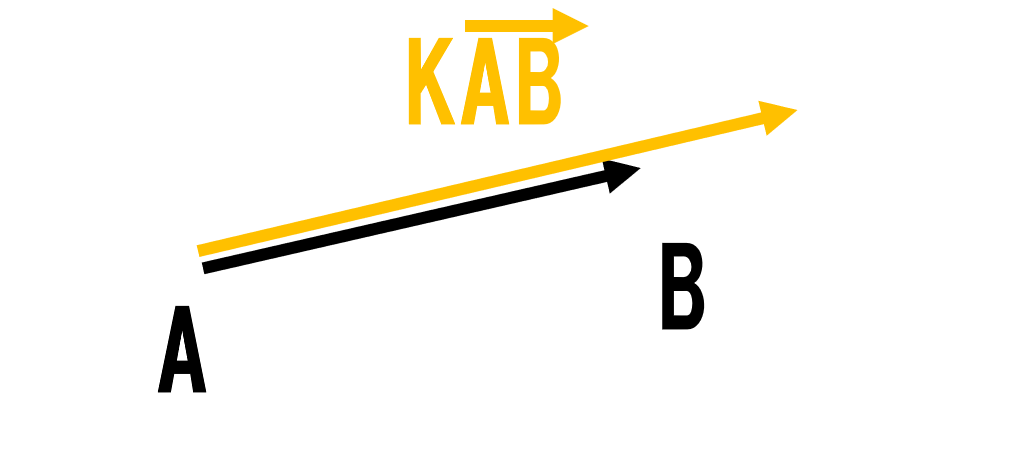
スカラー倍は伸び縮みさせると思ってください!
上の図はベクトルがk倍されて伸びているイメージです.
(ⅱ)k<0のときは逆の方向にk倍されるので下のようになります.
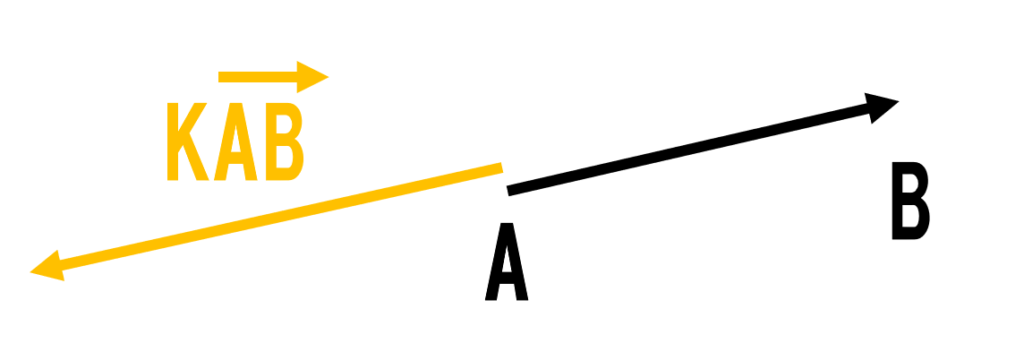
上の図はベクトルが逆方向にk倍されて伸びているイメージです.
このように和とスカラー倍でを定義しました!
この和とスカラーに対して一般に成り立つ法則を定理としてまとめます!
定理:ベクトルの和とスカラー倍
ベクトル\( \mathbf{a},\mathbf{b},\mathbf{c}\)と\( k,l \in \mathbb{R}\)に対して
以下のことが成り立つ.
(ベクトルの和について)
(ⅰ)\( \mathbf{a} + \mathbf{b}\) = \( \mathbf{b} + \mathbf{a}\)
(ⅱ)\( (\mathbf{a} + \mathbf{b}) + \mathbf{c} = \mathbf{a} + (\mathbf{b} + \mathbf{c})\)
(ⅲ)\( \mathbf{a} + \mathbf{0} = \mathbf{0} + \mathbf{a} = \mathbf{a}\)
(ⅳ)\( \mathbf{a} + (-\mathbf{a}) = (-\mathbf{a}) + \mathbf{a} = \mathbf{0}\)
(ベクトルのスカラー倍について)
(ⅴ)\( k( \mathbf{a} + \mathbf{b}) = k\mathbf{a} + k\mathbf{b}\)
(ⅵ) \( (k + l)\mathbf{a} = k\mathbf{a} + l\mathbf{a}\)
(ⅶ) \( k(l\mathbf{a}) = (kl)\mathbf{a}\)
以上がベクトルの演算の定理です!
何となく成り立ちそうなものが多いのではないでしょうか?
実数の世界とほとんど変わらない演算が施せます!
このベクトルの和とスカラー倍を用いて「ベクトルの成分表示」を考えたり
その他ベクトルの演算を行っていくことになりますので,
しっかりものにしてしまいましょう!
それではまとめに入ります!
「ベクトルの和とスカラー倍」まとめ
・ベクトルの和とは,\( \mathbf{c} = \mathbf{a} + \mathbf{b}\)
・ベクトルのスカラー倍とは\( k\mathbf{a}\)で伸縮を表している.

